Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 196084 by Mingma last updated on 17/Aug/23

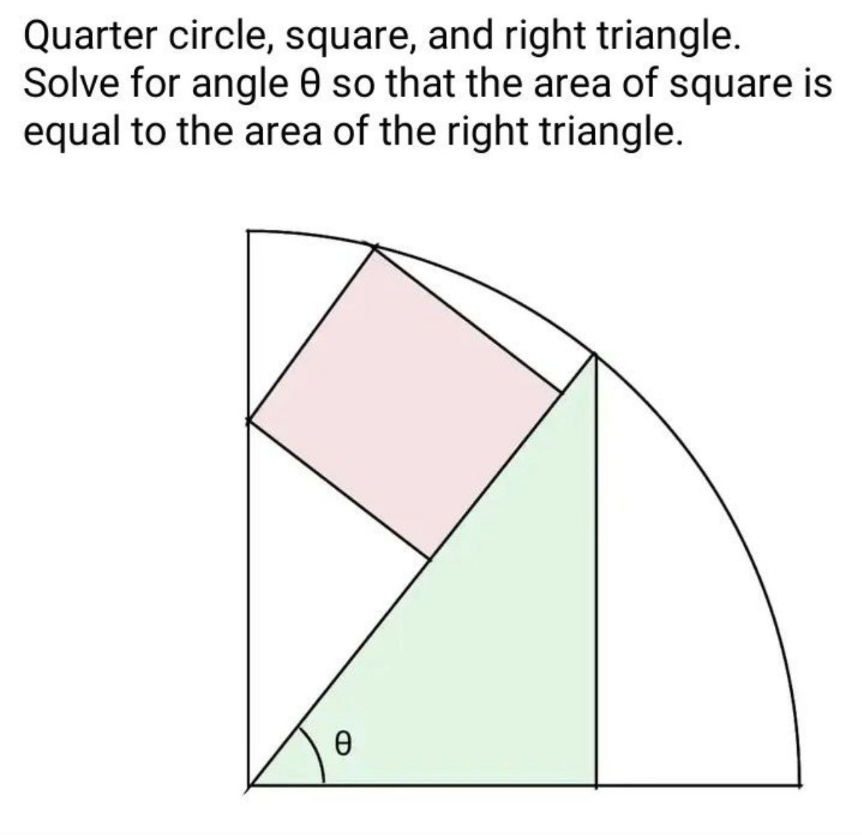
Answered by mr W last updated on 17/Aug/23

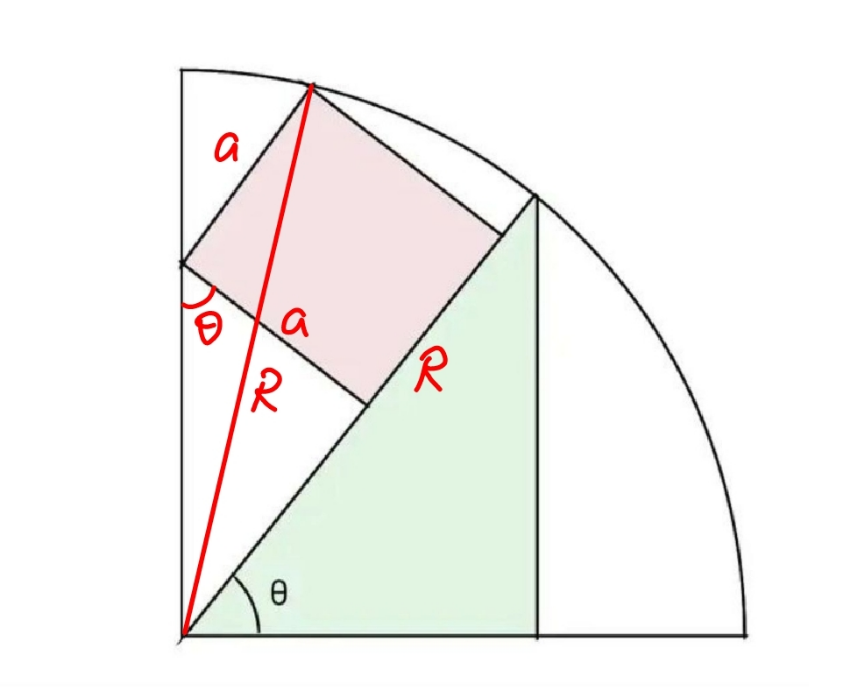
Commented by mr W last updated on 17/Aug/23

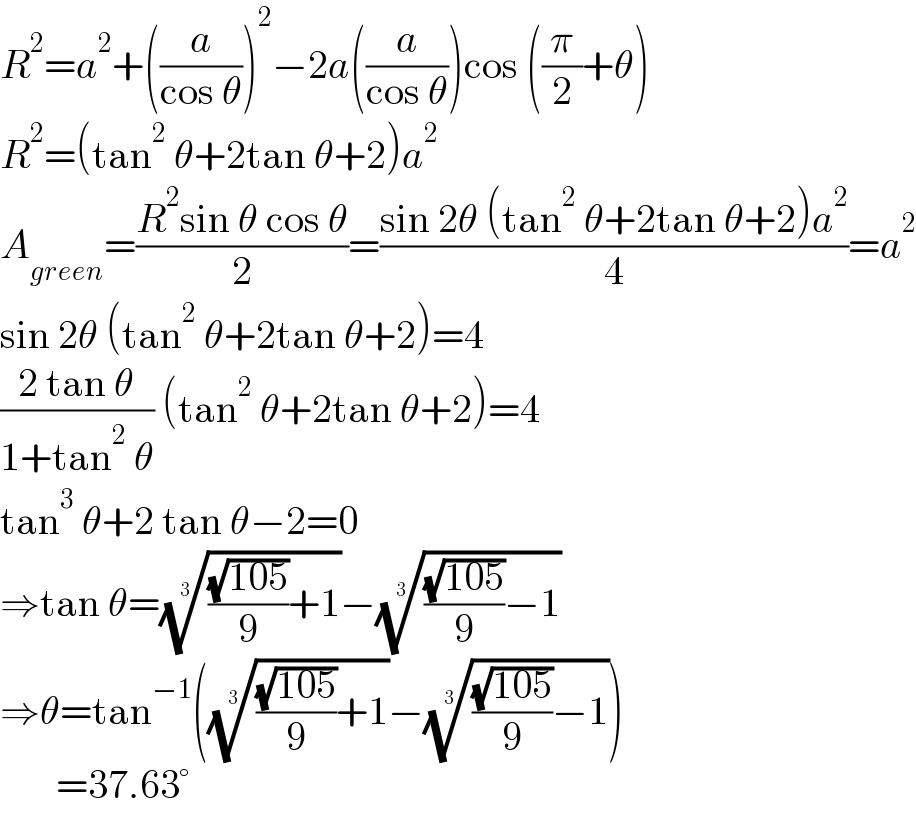
R^2 =a^2 +((a/(cos θ)))^2 −2a((a/(cos θ)))cos ((π/2)+θ) R^2 =(tan^2 θ+2tan θ+2)a^2 A_(green) =((R^2 sin θ cos θ)/2)=((sin 2θ (tan^2 θ+2tan θ+2)a^2 )/4)=a^2 sin 2θ (tan^2 θ+2tan θ+2)=4 ((2 tan θ)/(1+tan^2 θ)) (tan^2 θ+2tan θ+2)=4 tan^3 θ+2 tan θ−2=0 ⇒tan θ=((((√(105))/9)+1))^(1/3) −((((√(105))/9)−1))^(1/3) ⇒θ=tan^(−1) (((((√(105))/9)+1))^(1/3) −((((√(105))/9)−1))^(1/3) ) =37.63°

$${R}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left(\frac{{a}}{\mathrm{cos}\:\theta}\right)^{\mathrm{2}} −\mathrm{2}{a}\left(\frac{{a}}{\mathrm{cos}\:\theta}\right)\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}+\theta\right) \\ $$$${R}^{\mathrm{2}} =\left(\mathrm{tan}^{\mathrm{2}} \:\theta+\mathrm{2tan}\:\theta+\mathrm{2}\right){a}^{\mathrm{2}} \\ $$$${A}_{{green}} =\frac{{R}^{\mathrm{2}} \mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{2}}=\frac{\mathrm{sin}\:\mathrm{2}\theta\:\left(\mathrm{tan}^{\mathrm{2}} \:\theta+\mathrm{2tan}\:\theta+\mathrm{2}\right){a}^{\mathrm{2}} }{\mathrm{4}}={a}^{\mathrm{2}} \\ $$$$\mathrm{sin}\:\mathrm{2}\theta\:\left(\mathrm{tan}^{\mathrm{2}} \:\theta+\mathrm{2tan}\:\theta+\mathrm{2}\right)=\mathrm{4} \\ $$$$\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}\:\left(\mathrm{tan}^{\mathrm{2}} \:\theta+\mathrm{2tan}\:\theta+\mathrm{2}\right)=\mathrm{4} \\ $$$$\mathrm{tan}^{\mathrm{3}} \:\theta+\mathrm{2}\:\mathrm{tan}\:\theta−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{105}}}{\mathrm{9}}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{105}}}{\mathrm{9}}−\mathrm{1}} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \left(\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{105}}}{\mathrm{9}}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{105}}}{\mathrm{9}}−\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{37}.\mathrm{63}° \\ $$

Commented by Mingma last updated on 18/Aug/23

Perfect sir!

Terms of Service

Privacy Policy

Contact: info@tinkutara.com