Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

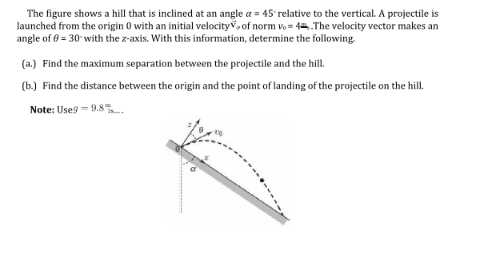
Question Number 195874 by Humble last updated on 12/Aug/23

Answered by mr W last updated on 12/Aug/23

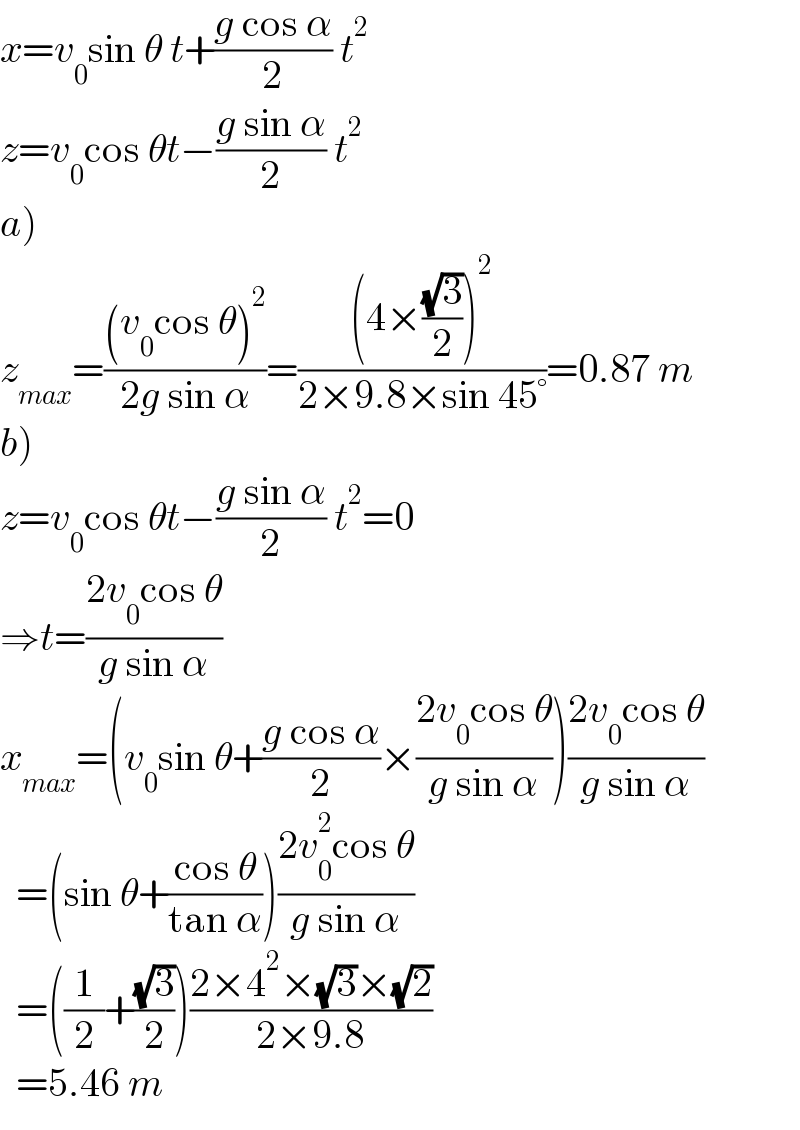
x=v_0 sin θ t+((g cos α)/2) t^2 z=v_0 cos θt−((g sin α)/2) t^2 a) z_(max) =(((v_0 cos θ)^2 )/(2g sin α))=(((4×((√3)/2))^2 )/(2×9.8×sin 45°))=0.87 m b) z=v_0 cos θt−((g sin α)/2) t^2 =0 ⇒t=((2v_0 cos θ)/(g sin α)) x_(max) =(v_0 sin θ+((g cos α)/2)×((2v_0 cos θ)/(g sin α)))((2v_0 cos θ)/(g sin α)) =(sin θ+((cos θ)/(tan α)))((2v_0 ^2 cos θ)/(g sin α)) =((1/2)+((√3)/2))((2×4^2 ×(√3)×(√2))/(2×9.8)) =5.46 m

$${x}={v}_{\mathrm{0}} \mathrm{sin}\:\theta\:{t}+\frac{{g}\:\mathrm{cos}\:\alpha}{\mathrm{2}}\:{t}^{\mathrm{2}} \\ $$$${z}={v}_{\mathrm{0}} \mathrm{cos}\:\theta{t}−\frac{{g}\:\mathrm{sin}\:\alpha}{\mathrm{2}}\:{t}^{\mathrm{2}} \\ $$$$\left.{a}\right) \\ $$$${z}_{{max}} =\frac{\left({v}_{\mathrm{0}} \mathrm{cos}\:\theta\right)^{\mathrm{2}} }{\mathrm{2}{g}\:\mathrm{sin}\:\alpha}=\frac{\left(\mathrm{4}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{9}.\mathrm{8}×\mathrm{sin}\:\mathrm{45}°}=\mathrm{0}.\mathrm{87}\:{m} \\ $$$$\left.{b}\right) \\ $$$${z}={v}_{\mathrm{0}} \mathrm{cos}\:\theta{t}−\frac{{g}\:\mathrm{sin}\:\alpha}{\mathrm{2}}\:{t}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{\mathrm{2}{v}_{\mathrm{0}} \mathrm{cos}\:\theta}{{g}\:\mathrm{sin}\:\alpha} \\ $$$${x}_{{max}} =\left({v}_{\mathrm{0}} \mathrm{sin}\:\theta+\frac{{g}\:\mathrm{cos}\:\alpha}{\mathrm{2}}×\frac{\mathrm{2}{v}_{\mathrm{0}} \mathrm{cos}\:\theta}{{g}\:\mathrm{sin}\:\alpha}\right)\frac{\mathrm{2}{v}_{\mathrm{0}} \mathrm{cos}\:\theta}{{g}\:\mathrm{sin}\:\alpha} \\ $$$$\:\:=\left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\alpha}\right)\frac{\mathrm{2}{v}_{\mathrm{0}} ^{\mathrm{2}} \mathrm{cos}\:\theta}{{g}\:\mathrm{sin}\:\alpha} \\ $$$$\:\:=\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\frac{\mathrm{2}×\mathrm{4}^{\mathrm{2}} ×\sqrt{\mathrm{3}}×\sqrt{\mathrm{2}}}{\mathrm{2}×\mathrm{9}.\mathrm{8}} \\ $$$$\:\:=\mathrm{5}.\mathrm{46}\:{m} \\ $$

Commented by Humble last updated on 12/Aug/23

Great! Thanks sir.

$$\mathrm{Great}! \\ $$$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com