Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

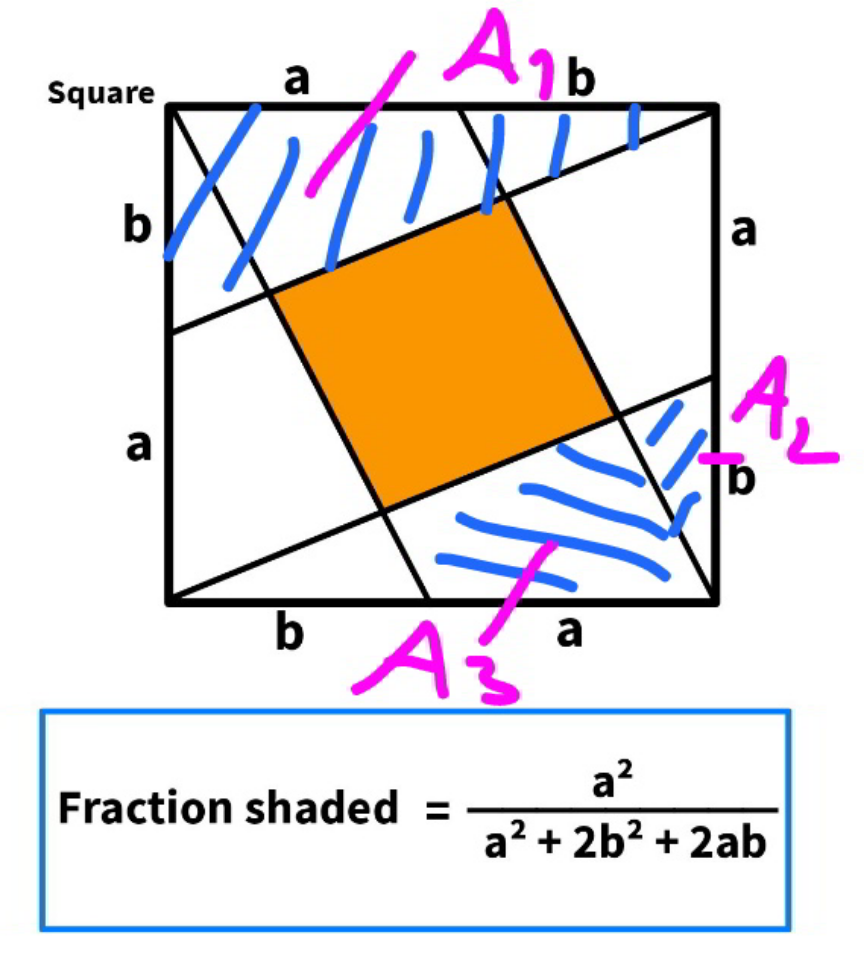
Question Number 195704 by sonukgindia last updated on 08/Aug/23

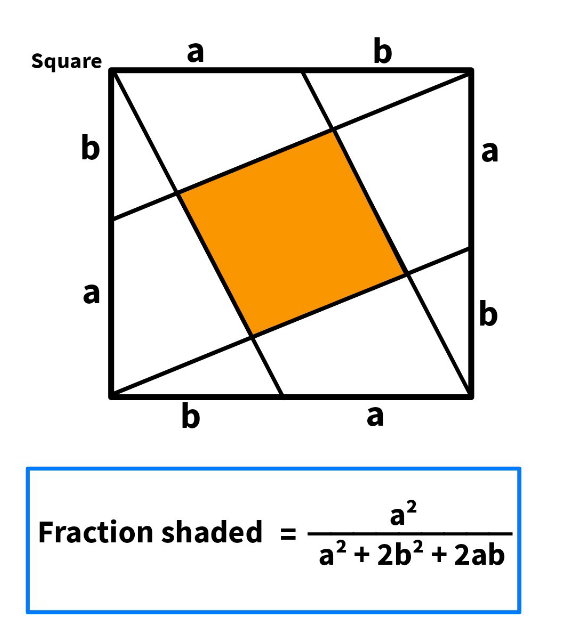
Answered by mr W last updated on 08/Aug/23

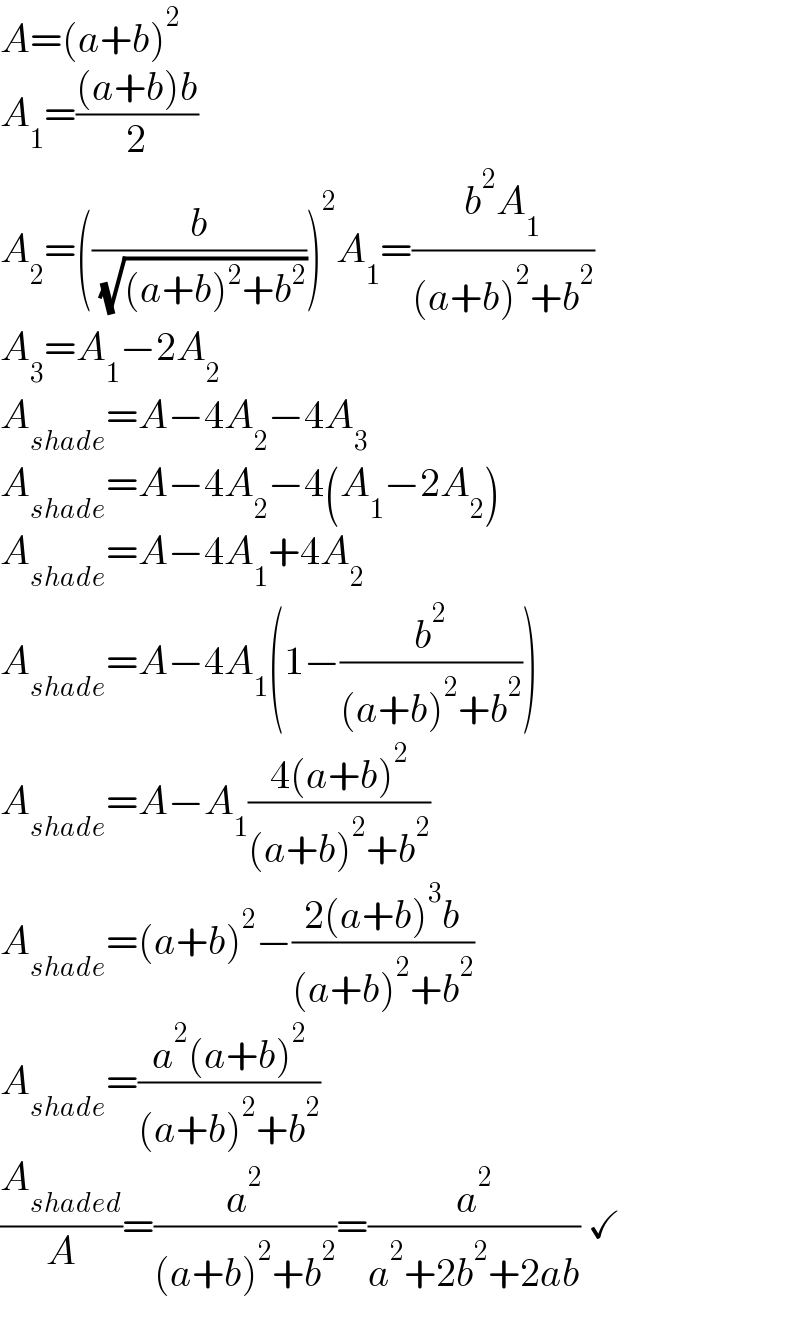
A=(a+b)^2 A_1 =(((a+b)b)/2) A_2 =((b/( (√((a+b)^2 +b^2 )))))^2 A_1 =((b^2 A_1 )/((a+b)^2 +b^2 )) A_3 =A_1 −2A_2 A_(shade) =A−4A_2 −4A_3 A_(shade) =A−4A_2 −4(A_1 −2A_2 ) A_(shade) =A−4A_1 +4A_2 A_(shade) =A−4A_1 (1−(b^2 /((a+b)^2 +b^2 ))) A_(shade) =A−A_1 ((4(a+b)^2 )/((a+b)^2 +b^2 )) A_(shade) =(a+b)^2 −((2(a+b)^3 b)/((a+b)^2 +b^2 )) A_(shade) =((a^2 (a+b)^2 )/((a+b)^2 +b^2 )) (A_(shaded) /A)=(a^2 /((a+b)^2 +b^2 ))=(a^2 /(a^2 +2b^2 +2ab)) ✓

$${A}=\left({a}+{b}\right)^{\mathrm{2}} \\ $$$${A}_{\mathrm{1}} =\frac{\left({a}+{b}\right){b}}{\mathrm{2}} \\ $$$${A}_{\mathrm{2}} =\left(\frac{{b}}{\:\sqrt{\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)^{\mathrm{2}} {A}_{\mathrm{1}} =\frac{{b}^{\mathrm{2}} {A}_{\mathrm{1}} }{\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${A}_{\mathrm{3}} ={A}_{\mathrm{1}} −\mathrm{2}{A}_{\mathrm{2}} \\ $$$${A}_{{shade}} ={A}−\mathrm{4}{A}_{\mathrm{2}} −\mathrm{4}{A}_{\mathrm{3}} \\ $$$${A}_{{shade}} ={A}−\mathrm{4}{A}_{\mathrm{2}} −\mathrm{4}\left({A}_{\mathrm{1}} −\mathrm{2}{A}_{\mathrm{2}} \right) \\ $$$${A}_{{shade}} ={A}−\mathrm{4}{A}_{\mathrm{1}} +\mathrm{4}{A}_{\mathrm{2}} \\ $$$${A}_{{shade}} ={A}−\mathrm{4}{A}_{\mathrm{1}} \left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} }\right) \\ $$$${A}_{{shade}} ={A}−{A}_{\mathrm{1}} \frac{\mathrm{4}\left({a}+{b}\right)^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${A}_{{shade}} =\left({a}+{b}\right)^{\mathrm{2}} −\frac{\mathrm{2}\left({a}+{b}\right)^{\mathrm{3}} {b}}{\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${A}_{{shade}} =\frac{{a}^{\mathrm{2}} \left({a}+{b}\right)^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\frac{{A}_{{shaded}} }{{A}}=\frac{{a}^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} }=\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{ab}}\:\checkmark \\ $$

Commented by mr W last updated on 08/Aug/23

Terms of Service

Privacy Policy

Contact: info@tinkutara.com