
Question Number 195688 by universe last updated on 07/Aug/23
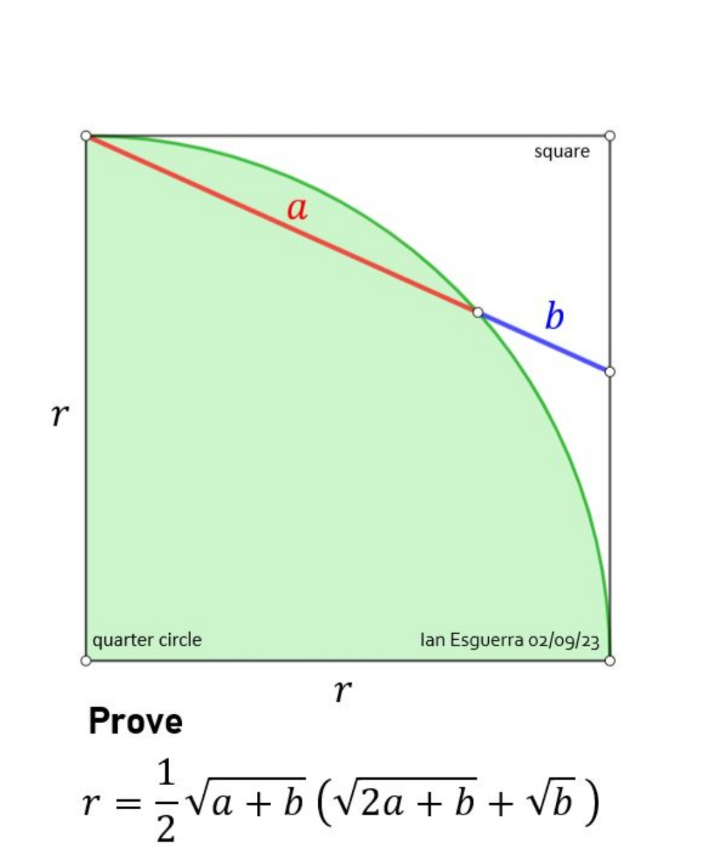
Answered by mr W last updated on 07/Aug/23
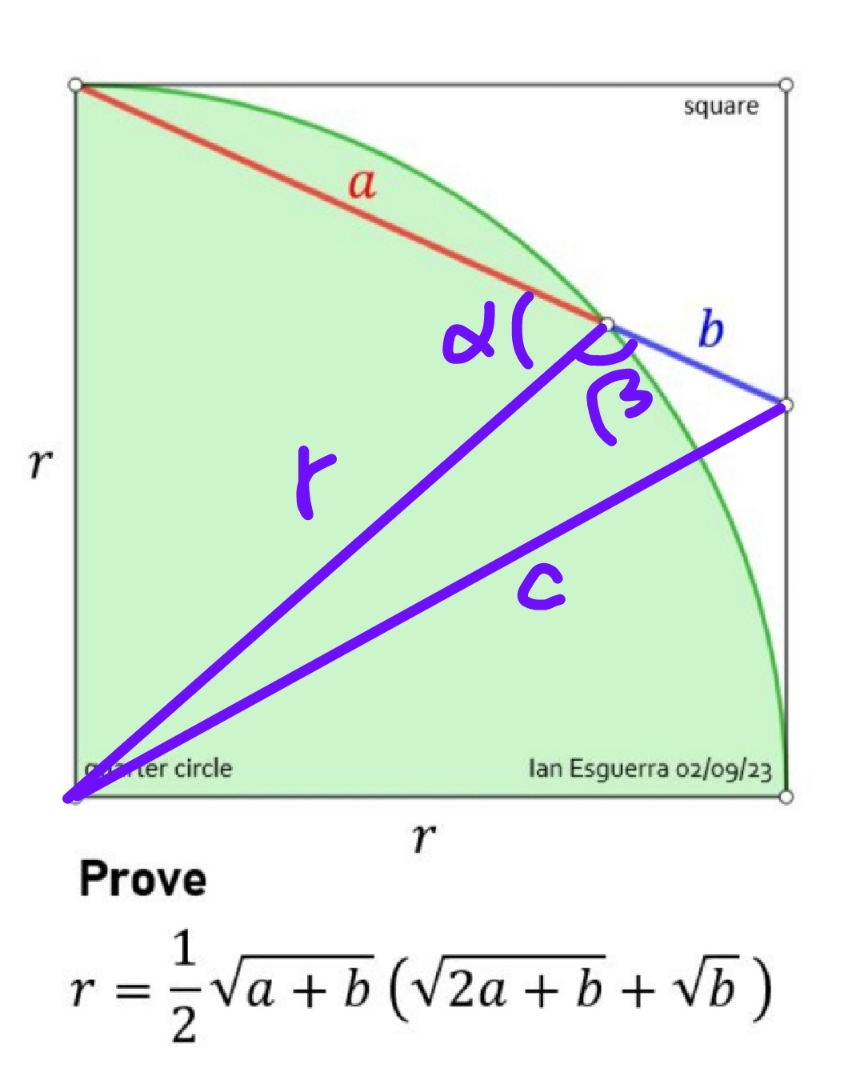
Commented by York12 last updated on 08/Aug/23
$${please}\:{bro}\:{try}\:{to}\:{remember} \\ $$
Commented by mr W last updated on 08/Aug/23
![c^2 =r^2 +(r−(√((a+b)^2 −r^2 )))^2 =r^2 +(a+b)^2 −2r(√((a+b)^2 −r^2 )) cos α=(a/(2r)) cos β=((r^2 +b^2 −c^2 )/(2rb)) cos α=−cos β (a/(2r))=−((r^2 +b^2 −c^2 )/(2rb)) a=((−r^2 −b^2 +r^2 +(a+b)^2 −2r(√((a+b)^2 −r^2 )))/b) 2r(√((a+b)^2 −r^2 ))=a(a+b) 4r^2 [(a+b)^2 −r^2 ]=a^2 (a+b)^2 4r^2 −4(a+b)^2 r^2 +a^2 (a+b)^2 =0 r^2 =(((a+b)[a+b+(√((2a+b)b))])/2) r^2 =(((a+b)((√(2a+b))+(√b))^2 )/4) ⇒r=(((√(a+b))((√(2a+b))+(√b)))/2) ✓](Q195691.png)
$${c}^{\mathrm{2}} ={r}^{\mathrm{2}} +\left({r}−\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }\right)^{\mathrm{2}} ={r}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{r}\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\mathrm{cos}\:\alpha=\frac{{a}}{\mathrm{2}{r}} \\ $$$$\mathrm{cos}\:\beta=\frac{{r}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{rb}} \\ $$$$\mathrm{cos}\:\alpha=−\mathrm{cos}\:\beta \\ $$$$\frac{{a}}{\mathrm{2}{r}}=−\frac{{r}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{rb}} \\ $$$${a}=\frac{−{r}^{\mathrm{2}} −{b}^{\mathrm{2}} +{r}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{r}\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }}{{b}} \\ $$$$\mathrm{2}{r}\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }={a}\left({a}+{b}\right) \\ $$$$\mathrm{4}{r}^{\mathrm{2}} \left[\left({a}+{b}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} \right]={a}^{\mathrm{2}} \left({a}+{b}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{r}^{\mathrm{2}} −\mathrm{4}\left({a}+{b}\right)^{\mathrm{2}} {r}^{\mathrm{2}} +{a}^{\mathrm{2}} \left({a}+{b}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${r}^{\mathrm{2}} =\frac{\left({a}+{b}\right)\left[{a}+{b}+\sqrt{\left(\mathrm{2}{a}+{b}\right){b}}\right]}{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} =\frac{\left({a}+{b}\right)\left(\sqrt{\mathrm{2}{a}+{b}}+\sqrt{{b}}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow{r}=\frac{\sqrt{{a}+{b}}\left(\sqrt{\mathrm{2}{a}+{b}}+\sqrt{{b}}\right)}{\mathrm{2}}\:\checkmark \\ $$
Commented by York12 last updated on 08/Aug/23
$${bro}\:{where}\:{to}\:{learn}\:{that} \\ $$
Commented by mr W last updated on 08/Aug/23

$${law}\:{of}\:{cosines}\:{in}\:{trigonometry}\:{is}\: \\ $$$${teached}\:{in}\:{every}\:{school}. \\ $$
Commented by York12 last updated on 08/Aug/23

$${no}\:{I}\:{do}\:{not}\:{talk}\:{about}\:{your}\:{solution} \\ $$$${I}\:\:{am}\:{asking}\:{what}\:{books}\:{you}\:{use}\:{in}\:{general} \\ $$
Commented by mr W last updated on 08/Aug/23

$${i}\:{can}\:{not}\:{remember}\:{any}\:{more}\:{what} \\ $$$${books}\:{i}\:{have}\:{used}.\:{nowadays}\:{i}\:{don}'{t} \\ $$$${use}\:{any}\:{book}.\:{if}\:{i}\:{want}\:{to}\:{get}\:{to}\:{know} \\ $$$${something},\:{i}\:{just}\:{ask}\:{google}. \\ $$
Commented by mr W last updated on 08/Aug/23
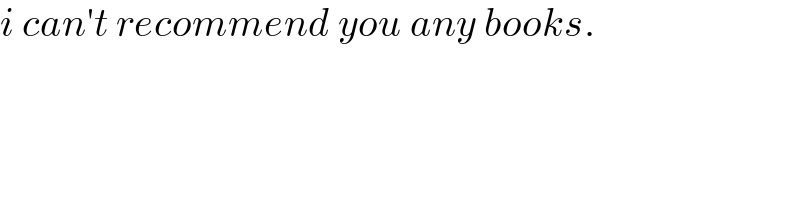
$${i}\:{can}'{t}\:{recommend}\:{you}\:{any}\:{books}. \\ $$
