
Question Number 195590 by Mingma last updated on 05/Aug/23
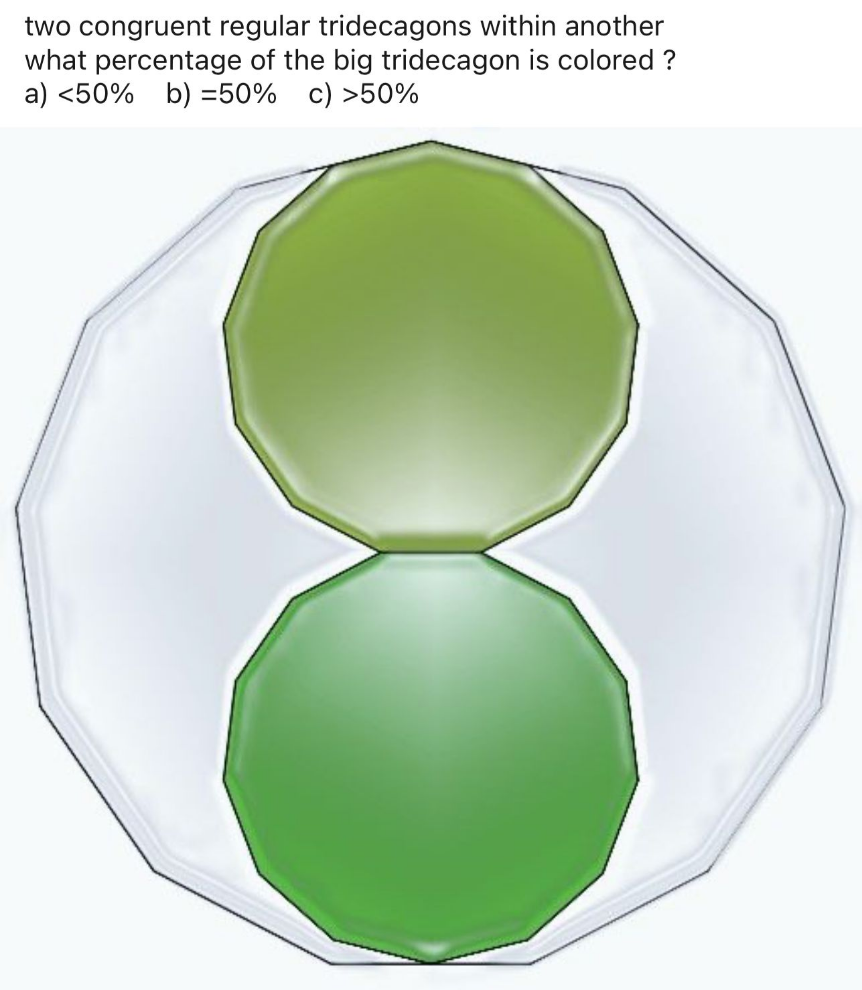
Answered by mr W last updated on 05/Aug/23

Commented by mr W last updated on 05/Aug/23

$$\frac{{H}}{{R}}=\mathrm{1}+\:\mathrm{cos}\:\frac{\mathrm{180}°}{\mathrm{13}}\approx\mathrm{1}.\mathrm{970942} \\ $$$${r}={radius}\:{of}\:{small}\:{tridecagons} \\ $$$${R}={radius}\:{of}\:{big}\:{tridecagon} \\ $$$${H}=\mathrm{2}{h} \\ $$$$\frac{{r}}{{R}}=\frac{{h}}{{H}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{area}\:{of}\:{small}\:{tridecagon}}{{area}\:{of}\:{big}\:{tridecagon}}=\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{{colored}\:{area}}{{big}\:{tridecagon}}=\frac{\mathrm{2}×{area}\:{of}\:{small}\:{tridecagon}}{{area}\:{of}\:{big}\:{tridecagon}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left.\Rightarrow{answer}\:{b}\right) \\ $$
Commented by Mingma last updated on 05/Aug/23
Perfect work, Prof
