
Question Number 195535 by arkanshh last updated on 04/Aug/23
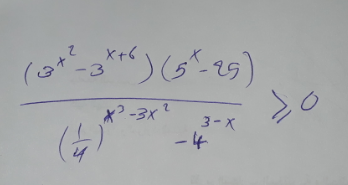
Answered by deleteduser1 last updated on 04/Aug/23
![((N=A×B)/D)=(((3^x^2 −3^(x+6) )(5^x −25))/(4^(x^2 (3−x)) −4^(3−x) ))≥0(Equality at x=2,−2) We use the fact that for inequality to be true, then N and D must have the same sign(+ve or −ve) Notice that x^2 (3−x)<3−x when x>3 (D<0,N>0) ⇒x>3 does not satisfy the inequality X x=3 also does not satisfy X When 1<x<3,D>0 2<x<3⇒N<0⇒2<x<3 does not satisfy X x=2 satisfies✓ 1<x<2⇒N>0⇒1<x≤2 satisfies✓ x=1 does not satisfy X When −1<x<1, D<0∧N<0 ⇒−1<x<1 satisfy✓;x=−1 does not satisfyX When −2<x<−1; D>0,B<0,A<0⇒N>0 ✓ When x<−2,D>0,N<0 X x∈[−2,−1)∪(−1,1)∪(1,2]](Q195537.png)
$$\frac{{N}={A}×{B}}{{D}}=\frac{\left(\mathrm{3}^{{x}^{\mathrm{2}} } −\mathrm{3}^{{x}+\mathrm{6}} \right)\left(\mathrm{5}^{{x}} −\mathrm{25}\right)}{\mathrm{4}^{{x}^{\mathrm{2}} \left(\mathrm{3}−{x}\right)} −\mathrm{4}^{\mathrm{3}−{x}} }\geqslant\mathrm{0}\left({Equality}\:{at}\:{x}=\mathrm{2},−\mathrm{2}\right) \\ $$$${We}\:{use}\:{the}\:{fact}\:{that}\:\:{for}\:{inequality}\:{to}\:{be}\:{true}, \\ $$$${then}\:{N}\:{and}\:{D}\:{must}\:{have}\:{the}\:{same}\:{sign}\left(+{ve}\:{or}\:−{ve}\right) \\ $$$${Notice}\:{that}\:{x}^{\mathrm{2}} \left(\mathrm{3}−{x}\right)<\mathrm{3}−{x}\:{when}\:{x}>\mathrm{3}\:\left({D}<\mathrm{0},{N}>\mathrm{0}\right) \\ $$$$\Rightarrow{x}>\mathrm{3}\:{does}\:{not}\:{satisfy}\:{the}\:{inequality}\:\:\:\:\:\:\:\:\:\:\:\:\:{X} \\ $$$${x}=\mathrm{3}\:{also}\:{does}\:{not}\:{satisfy}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{X} \\ $$$${When}\:\mathrm{1}<{x}<\mathrm{3},{D}>\mathrm{0} \\ $$$$\mathrm{2}<{x}<\mathrm{3}\Rightarrow{N}<\mathrm{0}\Rightarrow\mathrm{2}<{x}<\mathrm{3}\:{does}\:{not}\:{satisfy}\:\:\:\:\:\:{X} \\ $$$${x}=\mathrm{2}\:{satisfies}\checkmark \\ $$$$\mathrm{1}<{x}<\mathrm{2}\Rightarrow{N}>\mathrm{0}\Rightarrow\mathrm{1}<{x}\leqslant\mathrm{2}\:{satisfies}\checkmark \\ $$$${x}=\mathrm{1}\:{does}\:{not}\:{satisfy}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{X} \\ $$$${When}\:−\mathrm{1}<{x}<\mathrm{1},\:{D}<\mathrm{0}\wedge{N}<\mathrm{0} \\ $$$$\Rightarrow−\mathrm{1}<{x}<\mathrm{1}\:{satisfy}\checkmark;{x}=−\mathrm{1}\:{does}\:{not}\:{satisfyX} \\ $$$${When}\:−\mathrm{2}<{x}<−\mathrm{1};\:{D}>\mathrm{0},{B}<\mathrm{0},{A}<\mathrm{0}\Rightarrow{N}>\mathrm{0}\:\:\:\:\checkmark \\ $$$${When}\:{x}<−\mathrm{2},{D}>\mathrm{0},{N}<\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{X} \\ $$$${x}\in\left[−\mathrm{2},−\mathrm{1}\right)\cup\left(−\mathrm{1},\mathrm{1}\right)\cup\left(\mathrm{1},\mathrm{2}\right] \\ $$
Commented by arkanshh last updated on 04/Aug/23

$$ \\ $$$${woow}! \\ $$$${wonderfull}\:{sol}.\:{thnx}\:{for}\:{your}\:{time}. \\ $$
