
Question Number 195511 by Calculusboy last updated on 04/Aug/23
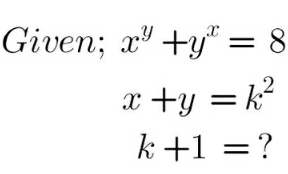
Answered by mr W last updated on 04/Aug/23
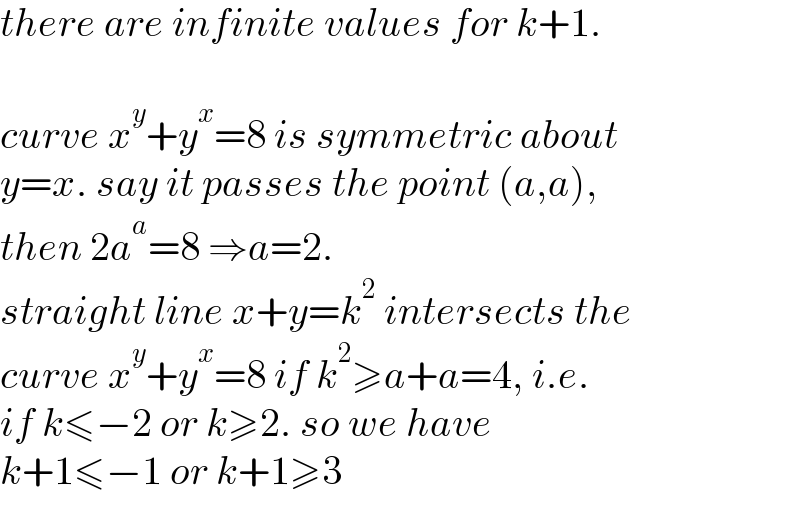
$${there}\:{are}\:{infinite}\:{values}\:{for}\:{k}+\mathrm{1}. \\ $$$$ \\ $$$${curve}\:{x}^{{y}} +{y}^{{x}} =\mathrm{8}\:{is}\:{symmetric}\:{about}\: \\ $$$${y}={x}.\:{say}\:{it}\:{passes}\:{the}\:{point}\:\left({a},{a}\right), \\ $$$${then}\:\mathrm{2}{a}^{{a}} =\mathrm{8}\:\Rightarrow{a}=\mathrm{2}. \\ $$$${straight}\:{line}\:{x}+{y}={k}^{\mathrm{2}} \:{intersects}\:{the} \\ $$$${curve}\:{x}^{{y}} +{y}^{{x}} =\mathrm{8}\:{if}\:{k}^{\mathrm{2}} \geqslant{a}+{a}=\mathrm{4},\:{i}.{e}. \\ $$$${if}\:{k}\leqslant−\mathrm{2}\:{or}\:{k}\geqslant\mathrm{2}.\:{so}\:{we}\:{have} \\ $$$${k}+\mathrm{1}\leqslant−\mathrm{1}\:{or}\:{k}+\mathrm{1}\geqslant\mathrm{3} \\ $$
Commented by Calculusboy last updated on 04/Aug/23

$${thanks}\:{sir} \\ $$
Commented by kapoorshah last updated on 05/Aug/23
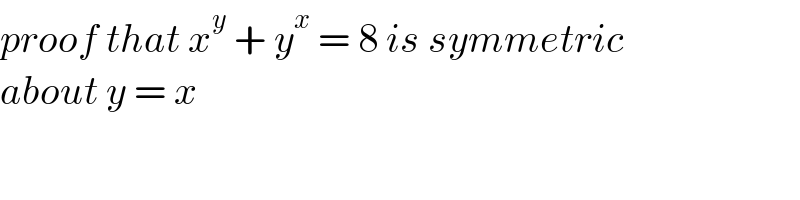
$${proof}\:{that}\:{x}^{{y}} \:+\:{y}^{{x}} \:=\:\mathrm{8}\:{is}\:{symmetric} \\ $$$${about}\:{y}\:=\:{x} \\ $$
Commented by mr W last updated on 05/Aug/23
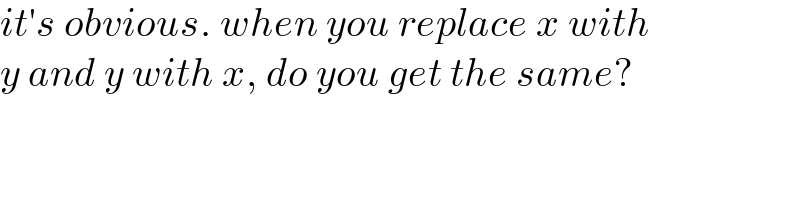
$${it}'{s}\:{obvious}.\:{when}\:{you}\:{replace}\:{x}\:{with} \\ $$$${y}\:{and}\:{y}\:{with}\:{x},\:{do}\:{you}\:{get}\:{the}\:{same}? \\ $$
