Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 195433 by sonukgindia last updated on 02/Aug/23

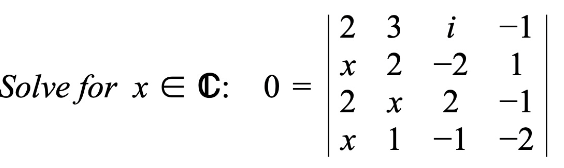
Answered by gatocomcirrose last updated on 02/Aug/23

2 determinant ((2,(−2),1),(x,2,(−1)),(1,(−1),(−2)))−3 determinant ((x,(−2),1),(2,2,(−1)),(x,(−1),(−2)))+ +i determinant ((x,2,1),(2,x,(−1)),(x,1,(−2)))+ determinant ((x,2,(−2)),(2,x,2),(x,1,(−1)))=0 ⇒2[−10−5x]−3[−5x−10]+i[−3x^2 −x+10]+[x^2 +2x]=0 ⇒x^2 (1−3i)+x(7−i)+10+10i=0 x=((i−7±(√(−110+66i)))/(2−6i))

$$\mathrm{2}\begin{vmatrix}{\mathrm{2}}&{−\mathrm{2}}&{\mathrm{1}}\\{\mathrm{x}}&{\mathrm{2}}&{−\mathrm{1}}\\{\mathrm{1}}&{−\mathrm{1}}&{−\mathrm{2}}\end{vmatrix}−\mathrm{3}\begin{vmatrix}{\mathrm{x}}&{−\mathrm{2}}&{\mathrm{1}}\\{\mathrm{2}}&{\mathrm{2}}&{−\mathrm{1}}\\{\mathrm{x}}&{−\mathrm{1}}&{−\mathrm{2}}\end{vmatrix}+ \\ $$$$+\mathrm{i}\begin{vmatrix}{\mathrm{x}}&{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{2}}&{\mathrm{x}}&{−\mathrm{1}}\\{\mathrm{x}}&{\mathrm{1}}&{−\mathrm{2}}\end{vmatrix}+\begin{vmatrix}{\mathrm{x}}&{\mathrm{2}}&{−\mathrm{2}}\\{\mathrm{2}}&{\mathrm{x}}&{\mathrm{2}}\\{\mathrm{x}}&{\mathrm{1}}&{−\mathrm{1}}\end{vmatrix}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left[−\mathrm{10}−\mathrm{5x}\right]−\mathrm{3}\left[−\mathrm{5x}−\mathrm{10}\right]+\mathrm{i}\left[−\mathrm{3x}^{\mathrm{2}} −\mathrm{x}+\mathrm{10}\right]+\left[\mathrm{x}^{\mathrm{2}} +\mathrm{2x}\right]=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3i}\right)+\mathrm{x}\left(\mathrm{7}−\mathrm{i}\right)+\mathrm{10}+\mathrm{10i}=\mathrm{0} \\ $$$$\mathrm{x}=\frac{\mathrm{i}−\mathrm{7}\pm\sqrt{−\mathrm{110}+\mathrm{66i}}}{\mathrm{2}−\mathrm{6i}} \\ $$

Commented by Frix last updated on 02/Aug/23

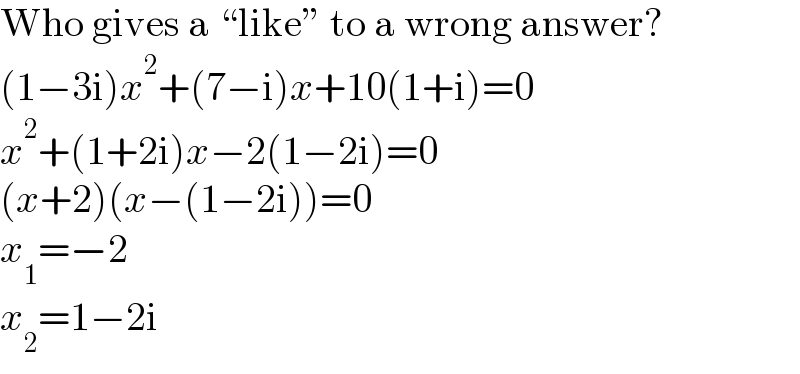
Who gives a “like” to a wrong answer? (1−3i)x^2 +(7−i)x+10(1+i)=0 x^2 +(1+2i)x−2(1−2i)=0 (x+2)(x−(1−2i))=0 x_1 =−2 x_2 =1−2i

$$\mathrm{Who}\:\mathrm{gives}\:\mathrm{a}\:``\mathrm{like}''\:\mathrm{to}\:\mathrm{a}\:\mathrm{wrong}\:\mathrm{answer}? \\ $$$$\left(\mathrm{1}−\mathrm{3i}\right){x}^{\mathrm{2}} +\left(\mathrm{7}−\mathrm{i}\right){x}+\mathrm{10}\left(\mathrm{1}+\mathrm{i}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{2i}\right){x}−\mathrm{2}\left(\mathrm{1}−\mathrm{2i}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{2}\right)\left({x}−\left(\mathrm{1}−\mathrm{2i}\right)\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =−\mathrm{2} \\ $$$${x}_{\mathrm{2}} =\mathrm{1}−\mathrm{2i} \\ $$

Commented by Frix last updated on 02/Aug/23

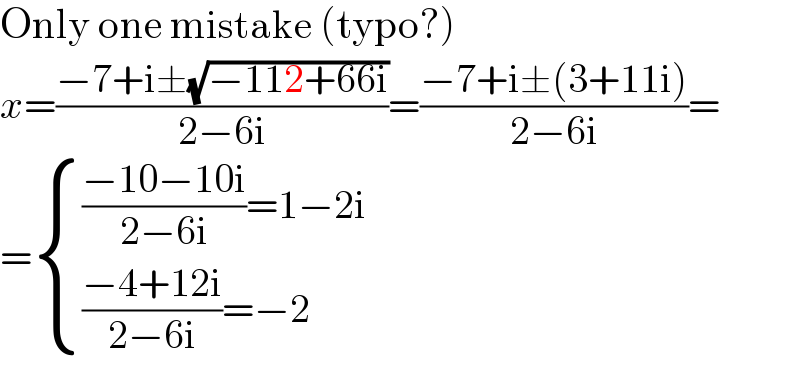
Only one mistake (typo?) x=((−7+i±(√(−112+66i)))/(2−6i))=((−7+i±(3+11i))/(2−6i))= = { ((((−10−10i)/(2−6i))=1−2i)),((((−4+12i)/(2−6i))=−2)) :}

$$\mathrm{Only}\:\mathrm{one}\:\mathrm{mistake}\:\left(\mathrm{typo}?\right) \\ $$$${x}=\frac{−\mathrm{7}+\mathrm{i}\pm\sqrt{−\mathrm{112}+\mathrm{66i}}}{\mathrm{2}−\mathrm{6i}}=\frac{−\mathrm{7}+\mathrm{i}\pm\left(\mathrm{3}+\mathrm{11i}\right)}{\mathrm{2}−\mathrm{6i}}= \\ $$$$=\begin{cases}{\frac{−\mathrm{10}−\mathrm{10i}}{\mathrm{2}−\mathrm{6i}}=\mathrm{1}−\mathrm{2i}}\\{\frac{−\mathrm{4}+\mathrm{12i}}{\mathrm{2}−\mathrm{6i}}=−\mathrm{2}}\end{cases} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com