Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 195415 by Calculusboy last updated on 02/Aug/23

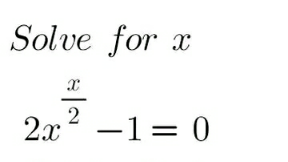
Answered by Frix last updated on 02/Aug/23

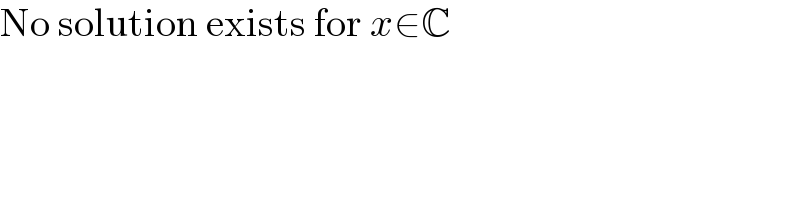
No solution exists for x∈C

$$\mathrm{No}\:\mathrm{solution}\:\mathrm{exists}\:\mathrm{for}\:{x}\in\mathbb{C} \\ $$

Commented by Frix last updated on 03/Aug/23

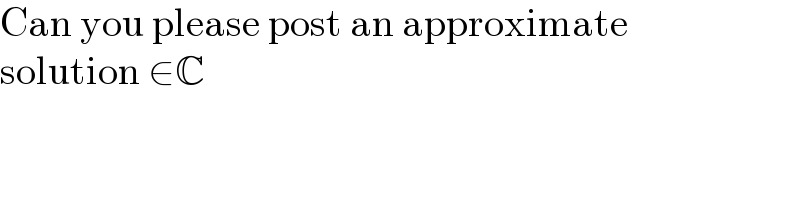
Can you please post an approximate solution ∈C

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{post}\:\mathrm{an}\:\mathrm{approximate} \\ $$$$\mathrm{solution}\:\in\mathbb{C} \\ $$

Commented by Calculusboy last updated on 03/Aug/23

thanks sir

$${thanks}\:{sir} \\ $$

Commented by mr W last updated on 03/Aug/23

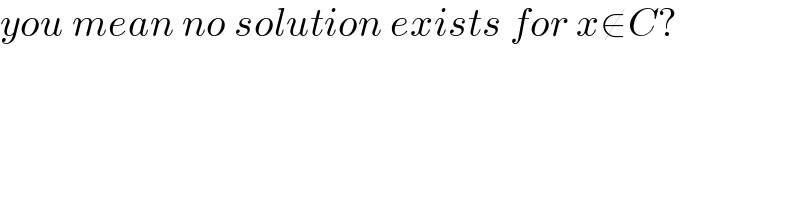
you mean no solution exists for x∉C?

$${you}\:{mean}\:{no}\:{solution}\:{exists}\:{for}\:{x}\notin{C}? \\ $$

Commented by Frix last updated on 04/Aug/23

...ok I was wrong, I just tried to approximate and got x≈.0535663+.913581i

$$...\mathrm{ok}\:\mathrm{I}\:\mathrm{was}\:\mathrm{wrong},\:\mathrm{I}\:\mathrm{just}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{approximate} \\ $$$$\mathrm{and}\:\mathrm{got} \\ $$$${x}\approx.\mathrm{0535663}+.\mathrm{913581i} \\ $$

Commented by Frix last updated on 04/Aug/23

The problem with x^x for x∈C: x=a+bi=(√(a^2 +b^2 ))e^(itan^(−1) (b/a)) =re^(iθ) x^x =(re^(iθ) )^(a+bi) =(((a^2 +b^2 )^(a/2) )/e^(btan^(−1) (b/a)) )×e^(i(((bln (a^2 +b^2 ))/2)+atan^(−1) (b/a))) and simply finding an exact real value for x^x ∈R with x∉R ⇔ b≠0 is not possible: ((bln (a^2 +b^2 ))/2)+atan^(−1) (b/a)=2nπ

$$\mathrm{The}\:\mathrm{problem}\:\mathrm{with}\:{x}^{{x}} \:\mathrm{for}\:{x}\in\mathbb{C}: \\ $$$${x}={a}+{b}\mathrm{i}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\mathrm{e}^{\mathrm{itan}^{−\mathrm{1}} \:\frac{{b}}{{a}}} ={r}\mathrm{e}^{\mathrm{i}\theta} \\ $$$${x}^{{x}} =\left({r}\mathrm{e}^{\mathrm{i}\theta} \right)^{{a}+{b}\mathrm{i}} =\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\frac{{a}}{\mathrm{2}}} }{\mathrm{e}^{{b}\mathrm{tan}^{−\mathrm{1}} \:\frac{{b}}{{a}}} }×\mathrm{e}^{\mathrm{i}\left(\frac{{b}\mathrm{ln}\:\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{\mathrm{2}}+{a}\mathrm{tan}^{−\mathrm{1}} \:\frac{{b}}{{a}}\right)} \\ $$$$\mathrm{and}\:\mathrm{simply}\:\mathrm{finding}\:\mathrm{an}\:\mathrm{exact}\:\mathrm{real}\:\mathrm{value}\:\mathrm{for} \\ $$$${x}^{{x}} \in\mathbb{R}\:\mathrm{with}\:{x}\notin\mathbb{R}\:\Leftrightarrow\:{b}\neq\mathrm{0}\:\mathrm{is}\:\mathrm{not}\:\mathrm{possible}: \\ $$$$\frac{{b}\mathrm{ln}\:\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{\mathrm{2}}+{a}\mathrm{tan}^{−\mathrm{1}} \:\frac{{b}}{{a}}=\mathrm{2}{n}\pi \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com