Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 195175 by valdirmd last updated on 25/Jul/23

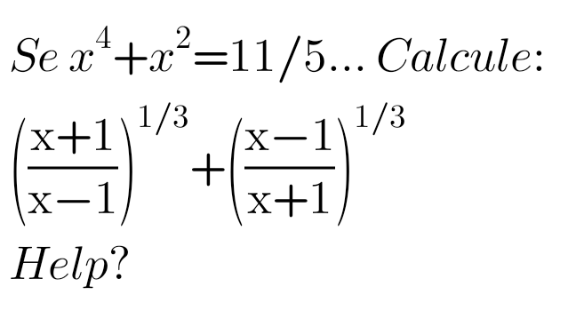
Answered by Rasheed.Sindhi last updated on 26/Jul/23

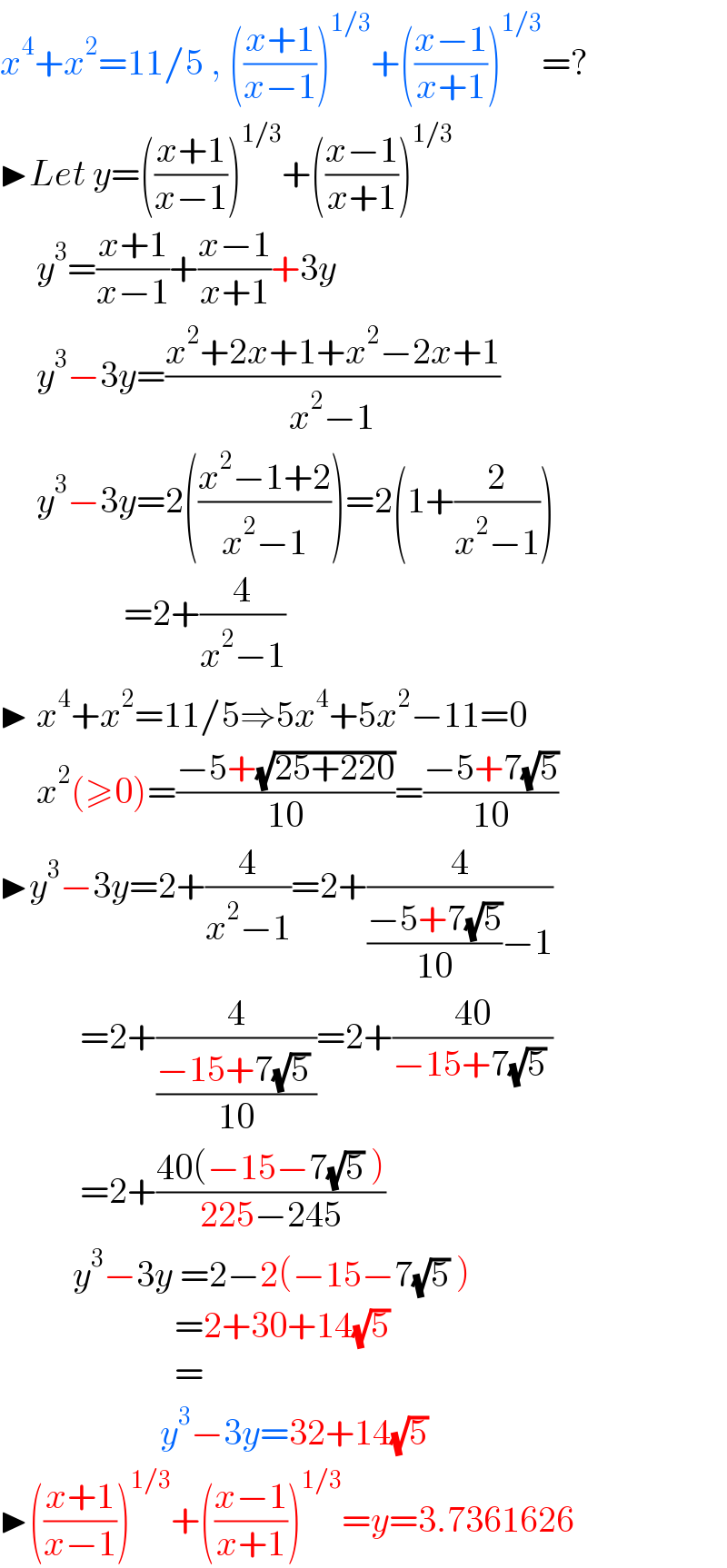
x^4 +x^2 =11/5 , (((x+1)/(x−1)))^(1/3) +(((x−1)/(x+1)))^(1/3) =? ▶Let y=(((x+1)/(x−1)))^(1/3) +(((x−1)/(x+1)))^(1/3) y^3 =((x+1)/(x−1))+((x−1)/(x+1))+3y y^3 −3y=((x^2 +2x+1+x^2 −2x+1)/(x^2 −1)) y^3 −3y=2(((x^2 −1+2)/(x^2 −1)))=2(1+(2/(x^2 −1))) =2+(4/(x^2 −1)) ▶ x^4 +x^2 =11/5⇒5x^4 +5x^2 −11=0 x^2 (≥0)=((−5+(√(25+220)))/(10))=((−5+7(√5))/(10)) ▶y^3 −3y=2+(4/(x^2 −1))=2+(4/(((−5+7(√5))/(10))−1)) =2+(4/((−15+7(√5) )/(10)))=2+((40)/(−15+7(√5) )) =2+((40(−15−7(√5) ))/(225−245)) y^3 −3y =2−2(−15−7(√5) ) =2+30+14(√5) = y^3 −3y=32+14(√5) ▶(((x+1)/(x−1)))^(1/3) +(((x−1)/(x+1)))^(1/3) =y=3.7361626

$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} =\mathrm{11}/\mathrm{5}\:,\:\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right)^{\mathrm{1}/\mathrm{3}} +\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{\mathrm{1}/\mathrm{3}} =? \\ $$$$\blacktriangleright{Let}\:{y}=\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right)^{\mathrm{1}/\mathrm{3}} +\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:\:\:{y}^{\mathrm{3}} =\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}+\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}+\mathrm{3}{y} \\ $$$$\:\:\:\:\:{y}^{\mathrm{3}} −\mathrm{3}{y}=\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:\:\:\:\:{y}^{\mathrm{3}} −\mathrm{3}{y}=\mathrm{2}\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}+\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}}\right)=\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}+\frac{\mathrm{4}}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\blacktriangleright\:{x}^{\mathrm{4}} +{x}^{\mathrm{2}} =\mathrm{11}/\mathrm{5}\Rightarrow\mathrm{5}{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{11}=\mathrm{0} \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} \left(\geqslant\mathrm{0}\right)=\frac{−\mathrm{5}+\sqrt{\mathrm{25}+\mathrm{220}}}{\mathrm{10}}=\frac{−\mathrm{5}+\mathrm{7}\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$$$\blacktriangleright{y}^{\mathrm{3}} −\mathrm{3}{y}=\mathrm{2}+\frac{\mathrm{4}}{{x}^{\mathrm{2}} −\mathrm{1}}=\mathrm{2}+\frac{\mathrm{4}}{\frac{−\mathrm{5}+\mathrm{7}\sqrt{\mathrm{5}}}{\mathrm{10}}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}+\frac{\mathrm{4}}{\frac{−\mathrm{15}+\mathrm{7}\sqrt{\mathrm{5}}\:}{\mathrm{10}}}=\mathrm{2}+\frac{\mathrm{40}}{−\mathrm{15}+\mathrm{7}\sqrt{\mathrm{5}}\:} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}+\frac{\mathrm{40}\left(−\mathrm{15}−\mathrm{7}\sqrt{\mathrm{5}}\:\right)}{\mathrm{225}−\mathrm{245}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{y}^{\mathrm{3}} −\mathrm{3}{y}\:=\mathrm{2}−\mathrm{2}\left(−\mathrm{15}−\mathrm{7}\sqrt{\mathrm{5}}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}+\mathrm{30}+\mathrm{14}\sqrt{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}^{\mathrm{3}} −\mathrm{3}{y}=\mathrm{32}+\mathrm{14}\sqrt{\mathrm{5}} \\ $$$$\blacktriangleright\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right)^{\mathrm{1}/\mathrm{3}} +\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{\mathrm{1}/\mathrm{3}} ={y}=\mathrm{3}.\mathrm{7361626} \\ $$

Commented by Rasheed.Sindhi last updated on 26/Jul/23

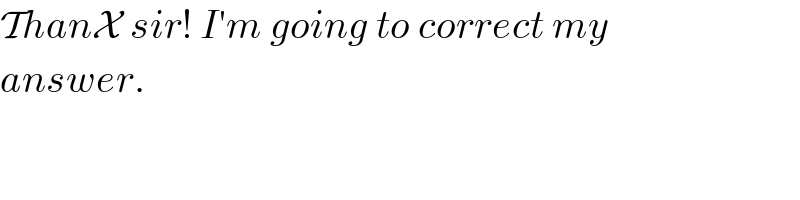
ThanX sir! I′m going to correct my answer.

$$\mathcal{T}{han}\mathcal{X}\:{sir}!\:{I}'{m}\:{going}\:{to}\:{correct}\:{my} \\ $$$${answer}. \\ $$

Commented by jihamine2301 last updated on 26/Jul/23

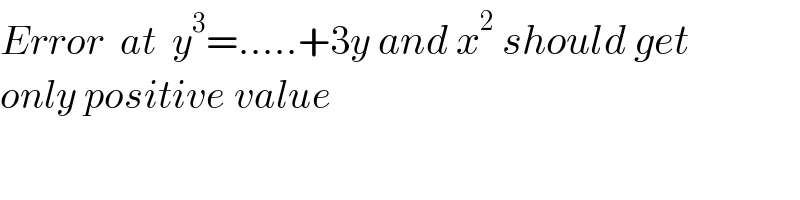
Error at y^3 =.....+3y and x^2 should get only positive value

$${Error}\:\:{at}\:\:{y}^{\mathrm{3}} =.....+\mathrm{3}{y}\:{and}\:{x}^{\mathrm{2}} \:{should}\:{get} \\ $$$${only}\:{positive}\:{value} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com