Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 194846 by dimentri last updated on 17/Jul/23

$$\:\:\:\:\:\:\underbrace{\:} \\ $$

Answered by som(math1967) last updated on 17/Jul/23

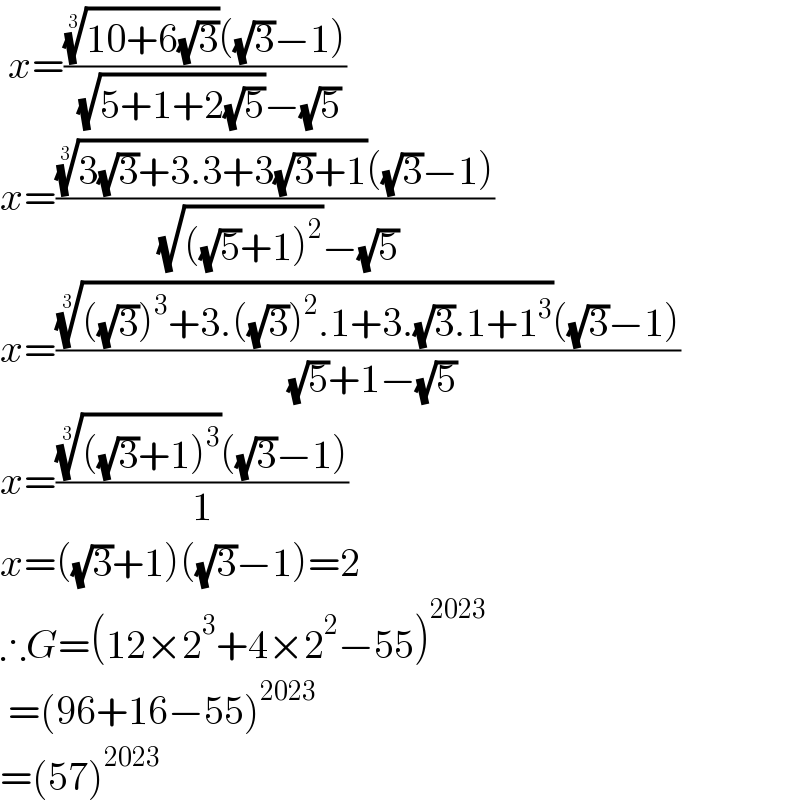
x=((((10+6(√3)))^(1/3) ((√3)−1))/( (√(5+1+2(√5)))−(√5))) x=((((3(√3)+3.3+3(√3)+1))^(1/3) ((√3)−1))/( (√(((√5)+1)^2 ))−(√5))) x=((((((√3))^3 +3.((√3))^2 .1+3.(√3).1+1^3 ))^(1/3) ((√3)−1))/( (√5)+1−(√5))) x=((((((√3)+1)^3 ))^(1/3) ((√3)−1))/1) x=((√3)+1)((√3)−1)=2 ∴G=(12×2^3 +4×2^2 −55)^(2023) =(96+16−55)^(2023) =(57)^(2023)

$$\:{x}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{10}+\mathrm{6}\sqrt{\mathrm{3}}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{5}+\mathrm{1}+\mathrm{2}\sqrt{\mathrm{5}}}−\sqrt{\mathrm{5}}} \\ $$$${x}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{3}.\mathrm{3}+\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{1}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\:\sqrt{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)^{\mathrm{2}} }−\sqrt{\mathrm{5}}} \\ $$$${x}=\frac{\sqrt[{\mathrm{3}}]{\left(\sqrt{\mathrm{3}}\right)^{\mathrm{3}} +\mathrm{3}.\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} .\mathrm{1}+\mathrm{3}.\sqrt{\mathrm{3}}.\mathrm{1}+\mathrm{1}^{\mathrm{3}} }\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{5}}+\mathrm{1}−\sqrt{\mathrm{5}}} \\ $$$${x}=\frac{\sqrt[{\mathrm{3}}]{\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)^{\mathrm{3}} }\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{1}} \\ $$$${x}=\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)=\mathrm{2} \\ $$$$\therefore{G}=\left(\mathrm{12}×\mathrm{2}^{\mathrm{3}} +\mathrm{4}×\mathrm{2}^{\mathrm{2}} −\mathrm{55}\right)^{\mathrm{2023}} \\ $$$$\:=\left(\mathrm{96}+\mathrm{16}−\mathrm{55}\right)^{\mathrm{2023}} \\ $$$$=\left(\mathrm{57}\right)^{\mathrm{2023}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com