
Question Number 194790 by BagusSetyoWibowo last updated on 15/Jul/23
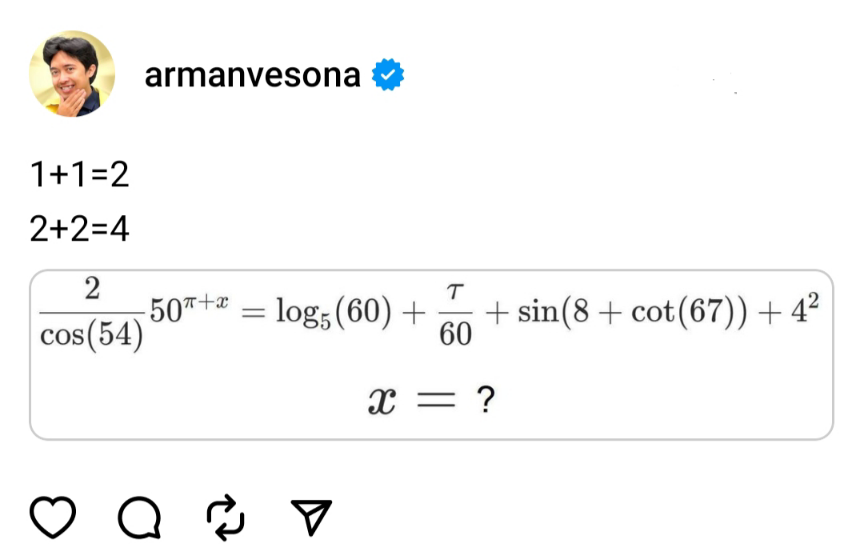
Answered by Frix last updated on 15/Jul/23
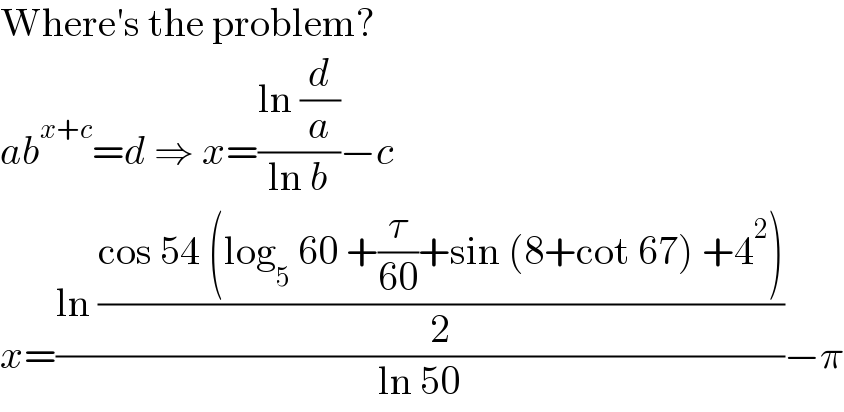
$$\mathrm{Where}'\mathrm{s}\:\mathrm{the}\:\mathrm{problem}? \\ $$$${ab}^{{x}+{c}} ={d}\:\Rightarrow\:{x}=\frac{\mathrm{ln}\:\frac{{d}}{{a}}}{\mathrm{ln}\:{b}}−{c} \\ $$$${x}=\frac{\mathrm{ln}\:\frac{\mathrm{cos}\:\mathrm{54}\:\left(\mathrm{log}_{\mathrm{5}} \:\mathrm{60}\:+\frac{\tau}{\mathrm{60}}+\mathrm{sin}\:\left(\mathrm{8}+\mathrm{cot}\:\mathrm{67}\right)\:+\mathrm{4}^{\mathrm{2}} \right)}{\mathrm{2}}}{\mathrm{ln}\:\mathrm{50}}−\pi \\ $$
