Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 194732 by MathsFan last updated on 14/Jul/23

Commented by York12 last updated on 15/Jul/23

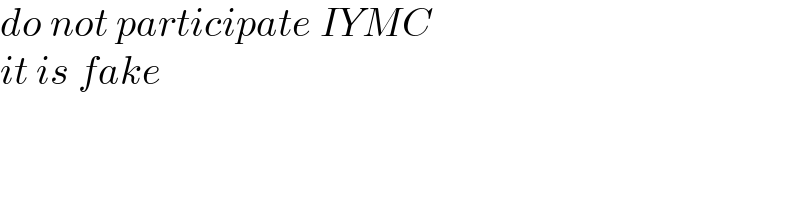
do not participate IYMC it is fake

$${do}\:{not}\:{participate}\:{IYMC} \\ $$$${it}\:{is}\:{fake} \\ $$

Answered by mahdipoor last updated on 14/Jul/23

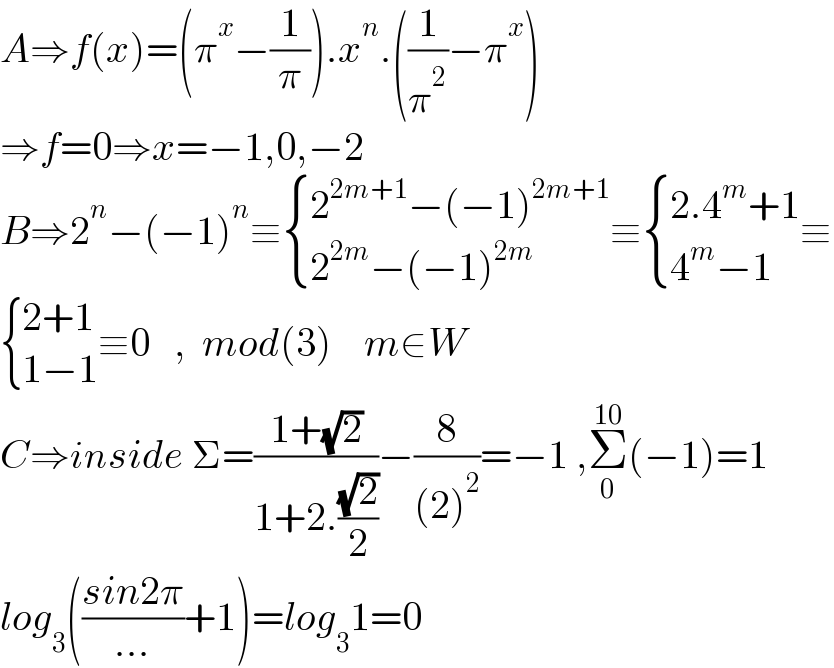
A⇒f(x)=(π^x −(1/π)).x^n .((1/π^2 )−π^x ) ⇒f=0⇒x=−1,0,−2 B⇒2^n −(−1)^n ≡ { ((2^(2m+1) −(−1)^(2m+1) )),((2^(2m) −(−1)^(2m) )) :}≡ { ((2.4^m +1)),((4^m −1)) :}≡ { ((2+1)),((1−1)) :}≡0 , mod(3) m∈W C⇒inside Σ=((1+(√2))/(1+2.((√2)/2)))−(8/((2)^2 ))=−1 ,Σ_0 ^(10) (−1)=1 log_3 (((sin2π)/(...))+1)=log_3 1=0

$${A}\Rightarrow{f}\left({x}\right)=\left(\pi^{{x}} −\frac{\mathrm{1}}{\pi}\right).{x}^{{n}} .\left(\frac{\mathrm{1}}{\pi^{\mathrm{2}} }−\pi^{{x}} \right) \\ $$$$\Rightarrow{f}=\mathrm{0}\Rightarrow{x}=−\mathrm{1},\mathrm{0},−\mathrm{2} \\ $$$${B}\Rightarrow\mathrm{2}^{{n}} −\left(−\mathrm{1}\right)^{{n}} \equiv\begin{cases}{\mathrm{2}^{\mathrm{2}{m}+\mathrm{1}} −\left(−\mathrm{1}\right)^{\mathrm{2}{m}+\mathrm{1}} }\\{\mathrm{2}^{\mathrm{2}{m}} −\left(−\mathrm{1}\right)^{\mathrm{2}{m}} }\end{cases}\equiv\begin{cases}{\mathrm{2}.\mathrm{4}^{{m}} +\mathrm{1}}\\{\mathrm{4}^{{m}} −\mathrm{1}}\end{cases}\equiv \\ $$$$\begin{cases}{\mathrm{2}+\mathrm{1}}\\{\mathrm{1}−\mathrm{1}}\end{cases}\equiv\mathrm{0}\:\:\:,\:\:{mod}\left(\mathrm{3}\right)\:\:\:\:{m}\in{W}\:\:\:\: \\ $$$${C}\Rightarrow{inside}\:\Sigma=\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{1}+\mathrm{2}.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}−\frac{\mathrm{8}}{\left(\mathrm{2}\right)^{\mathrm{2}} }=−\mathrm{1}\:,\underset{\mathrm{0}} {\overset{\mathrm{10}} {\sum}}\left(−\mathrm{1}\right)=\mathrm{1} \\ $$$${log}_{\mathrm{3}} \left(\frac{{sin}\mathrm{2}\pi}{...}+\mathrm{1}\right)={log}_{\mathrm{3}} \mathrm{1}=\mathrm{0} \\ $$

Commented by York12 last updated on 15/Jul/23

bro it is an onlie exam called IYMC & he is cheating

$${bro}\:{it}\:{is}\:{an}\:{onlie}\:{exam}\: \\ $$$${called}\:{IYMC}\:\&\:{he}\:{is}\:{cheating} \\ $$

Answered by qaz last updated on 15/Jul/23

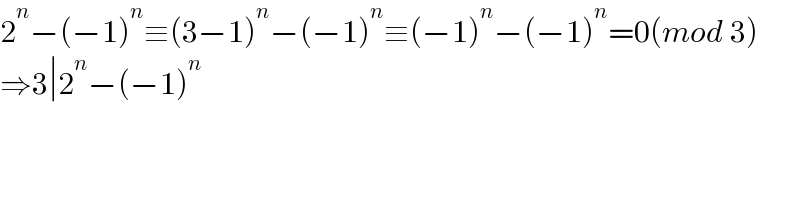
2^n −(−1)^n ≡(3−1)^n −(−1)^n ≡(−1)^n −(−1)^n =0(mod 3) ⇒3∣2^n −(−1)^n

$$\mathrm{2}^{{n}} −\left(−\mathrm{1}\right)^{{n}} \equiv\left(\mathrm{3}−\mathrm{1}\right)^{{n}} −\left(−\mathrm{1}\right)^{{n}} \equiv\left(−\mathrm{1}\right)^{{n}} −\left(−\mathrm{1}\right)^{{n}} =\mathrm{0}\left({mod}\:\mathrm{3}\right) \\ $$$$\Rightarrow\mathrm{3}\mid\mathrm{2}^{{n}} −\left(−\mathrm{1}\right)^{{n}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com