
Question Number 194455 by Spillover last updated on 07/Jul/23
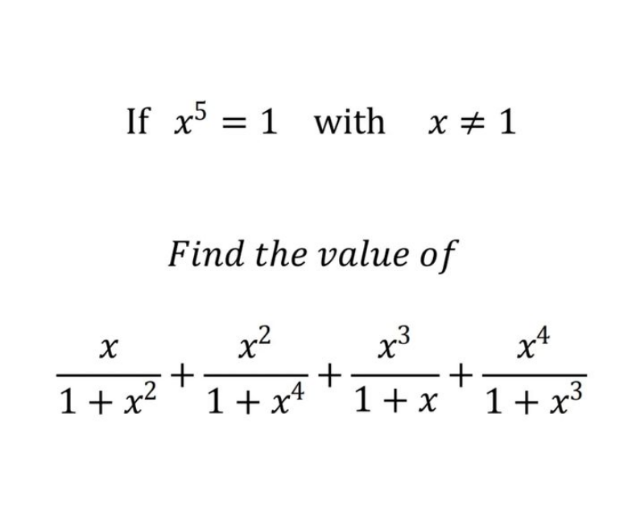
Answered by qaz last updated on 07/Jul/23
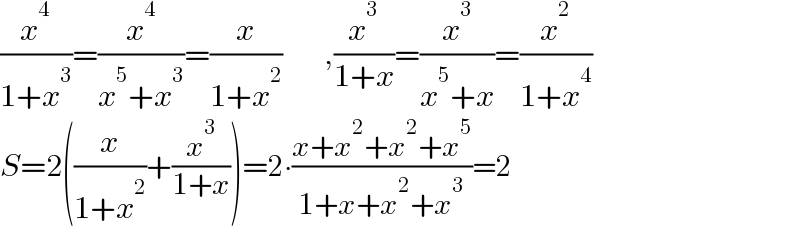
$$\frac{{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{3}} }=\frac{{x}^{\mathrm{4}} }{{x}^{\mathrm{5}} +{x}^{\mathrm{3}} }=\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:\:\:\:\:\:,\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}}=\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{5}} +{x}}=\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{4}} } \\ $$$${S}=\mathrm{2}\left(\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }+\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}}\right)=\mathrm{2}\centerdot\frac{{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{2}} +{x}^{\mathrm{5}} }{\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }=\mathrm{2} \\ $$
