
Question Number 194088 by cortano12 last updated on 27/Jun/23
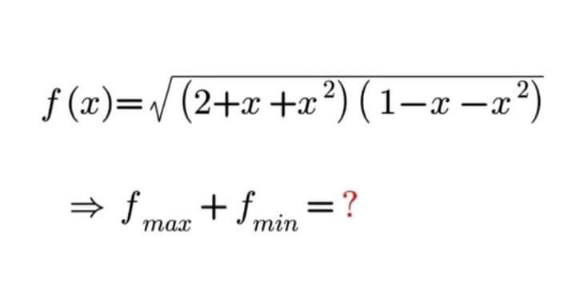
Answered by horsebrand11 last updated on 27/Jun/23
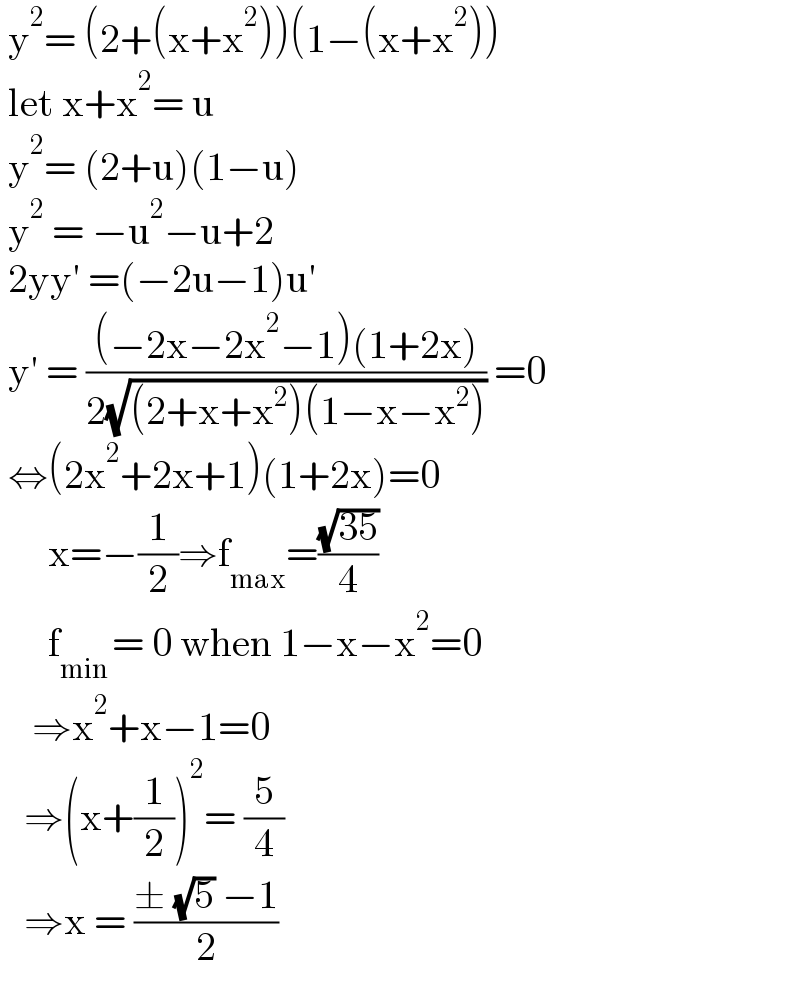
$$\:\mathrm{y}^{\mathrm{2}} =\:\left(\mathrm{2}+\left(\mathrm{x}+\mathrm{x}^{\mathrm{2}} \right)\right)\left(\mathrm{1}−\left(\mathrm{x}+\mathrm{x}^{\mathrm{2}} \right)\right) \\ $$$$\:\mathrm{let}\:\mathrm{x}+\mathrm{x}^{\mathrm{2}} =\:\mathrm{u} \\ $$$$\:\mathrm{y}^{\mathrm{2}} =\:\left(\mathrm{2}+\mathrm{u}\right)\left(\mathrm{1}−\mathrm{u}\right) \\ $$$$\:\mathrm{y}^{\mathrm{2}} \:=\:−\mathrm{u}^{\mathrm{2}} −\mathrm{u}+\mathrm{2} \\ $$$$\:\mathrm{2yy}'\:=\left(−\mathrm{2u}−\mathrm{1}\right)\mathrm{u}'\: \\ $$$$\:\mathrm{y}'\:=\:\frac{\left(−\mathrm{2x}−\mathrm{2x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{1}+\mathrm{2x}\right)}{\mathrm{2}\sqrt{\left(\mathrm{2}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{x}−\mathrm{x}^{\mathrm{2}} \right)}}\:=\mathrm{0} \\ $$$$\:\Leftrightarrow\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{2x}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{x}=−\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{f}_{\mathrm{max}} =\frac{\sqrt{\mathrm{35}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\mathrm{f}_{\mathrm{min}\:} =\:\mathrm{0}\:\mathrm{when}\:\mathrm{1}−\mathrm{x}−\mathrm{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\Rightarrow\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\:\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\:\:\:\Rightarrow\mathrm{x}\:=\:\frac{\pm\:\sqrt{\mathrm{5}}\:−\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 27/Jun/23

$${mercey}\:{sir} \\ $$
Answered by Frix last updated on 27/Jun/23

$$\mathrm{0}\leqslant{f}\left({x}\right)\leqslant\frac{\sqrt{\mathrm{35}}}{\mathrm{4}} \\ $$
Answered by Subhi last updated on 27/Jun/23
![(1−x−x^2 ) ⇛ max value at f(((−b)/(2a)))=f(((−1)/2))=(5/4) (√((1−x−x^2 )(2+x+x^2 ))) ⇛ 1−x−x^2 ≥0 ∴ the mini value is 0 x^2 +x−1≤0 (x−((−1+(√5))/2))(x+((1+(√5))/2))≤0 x ∈ [((−1−(√5))/2),((−1+(√5))/2)] f_(max) is at x=((−1)/2) , gives the max value of (1−x−x^2 ) f_(max) =(√((5/4).(7/4)))= ((√(35))/4) f_(max) +f_(mini) = ((√(35))/4)](Q194093.png)
$$\left(\mathrm{1}−{x}−{x}^{\mathrm{2}} \right)\:\Rrightarrow\:{max}\:{value}\:{at}\:{f}\left(\frac{−{b}}{\mathrm{2}{a}}\right)={f}\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\sqrt{\left(\mathrm{1}−{x}−{x}^{\mathrm{2}} \right)\left(\mathrm{2}+{x}+{x}^{\mathrm{2}} \right)}\:\Rrightarrow\:\mathrm{1}−{x}−{x}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\therefore\:{the}\:{mini}\:{value}\:{is}\:\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{x}−\mathrm{1}\leqslant\mathrm{0} \\ $$$$\left({x}−\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\leqslant\mathrm{0} \\ $$$${x}\:\in\:\left[\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}},\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right] \\ $$$${f}_{{max}} \:{is}\:{at}\:{x}=\frac{−\mathrm{1}}{\mathrm{2}}\:,\:{gives}\:{the}\:{max}\:{value}\:{of}\:\left(\mathrm{1}−{x}−{x}^{\mathrm{2}} \right) \\ $$$${f}_{{max}} =\sqrt{\frac{\mathrm{5}}{\mathrm{4}}.\frac{\mathrm{7}}{\mathrm{4}}}=\:\frac{\sqrt{\mathrm{35}}}{\mathrm{4}} \\ $$$${f}_{{max}} +{f}_{{mini}} \:=\:\frac{\sqrt{\mathrm{35}}}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 27/Jun/23

$${perfect}\:{sir} \\ $$
