
Question Number 193972 by Rupesh123 last updated on 24/Jun/23

Commented by Frix last updated on 25/Jun/23

$$\mathrm{Ok}\:\mathrm{I}\:\mathrm{thought}\:\mathrm{about}\:\mathrm{it}.\:\mathrm{What}\:\mathrm{now}? \\ $$
Commented by Rupesh123 last updated on 25/Jun/23
Can you tell me what you thought?
Commented by Rajpurohith last updated on 25/Jun/23
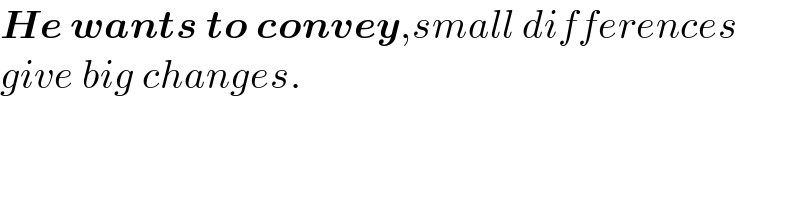
$$\boldsymbol{{He}}\:\boldsymbol{{wants}}\:\boldsymbol{{to}}\:\boldsymbol{{convey}},{small}\:{differences} \\ $$$${give}\:{big}\:{changes}. \\ $$
Commented by Frix last updated on 26/Jun/23
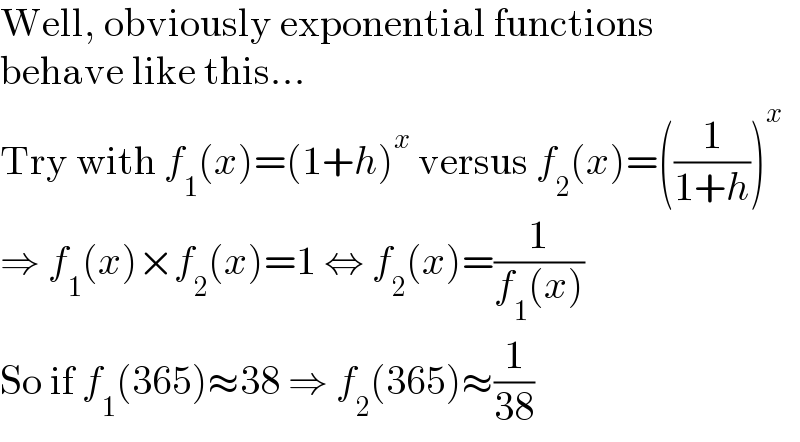
$$\mathrm{Well},\:\mathrm{obviously}\:\mathrm{exponential}\:\mathrm{functions} \\ $$$$\mathrm{behave}\:\mathrm{like}\:\mathrm{this}... \\ $$$$\mathrm{Try}\:\mathrm{with}\:{f}_{\mathrm{1}} \left({x}\right)=\left(\mathrm{1}+{h}\right)^{{x}} \:\mathrm{versus}\:{f}_{\mathrm{2}} \left({x}\right)=\left(\frac{\mathrm{1}}{\mathrm{1}+{h}}\right)^{{x}} \\ $$$$\Rightarrow\:{f}_{\mathrm{1}} \left({x}\right)×{f}_{\mathrm{2}} \left({x}\right)=\mathrm{1}\:\Leftrightarrow\:{f}_{\mathrm{2}} \left({x}\right)=\frac{\mathrm{1}}{{f}_{\mathrm{1}} \left({x}\right)} \\ $$$$\mathrm{So}\:\mathrm{if}\:{f}_{\mathrm{1}} \left(\mathrm{365}\right)\approx\mathrm{38}\:\Rightarrow\:{f}_{\mathrm{2}} \left(\mathrm{365}\right)\approx\frac{\mathrm{1}}{\mathrm{38}} \\ $$
