
Question Number 193686 by Rupesh123 last updated on 18/Jun/23
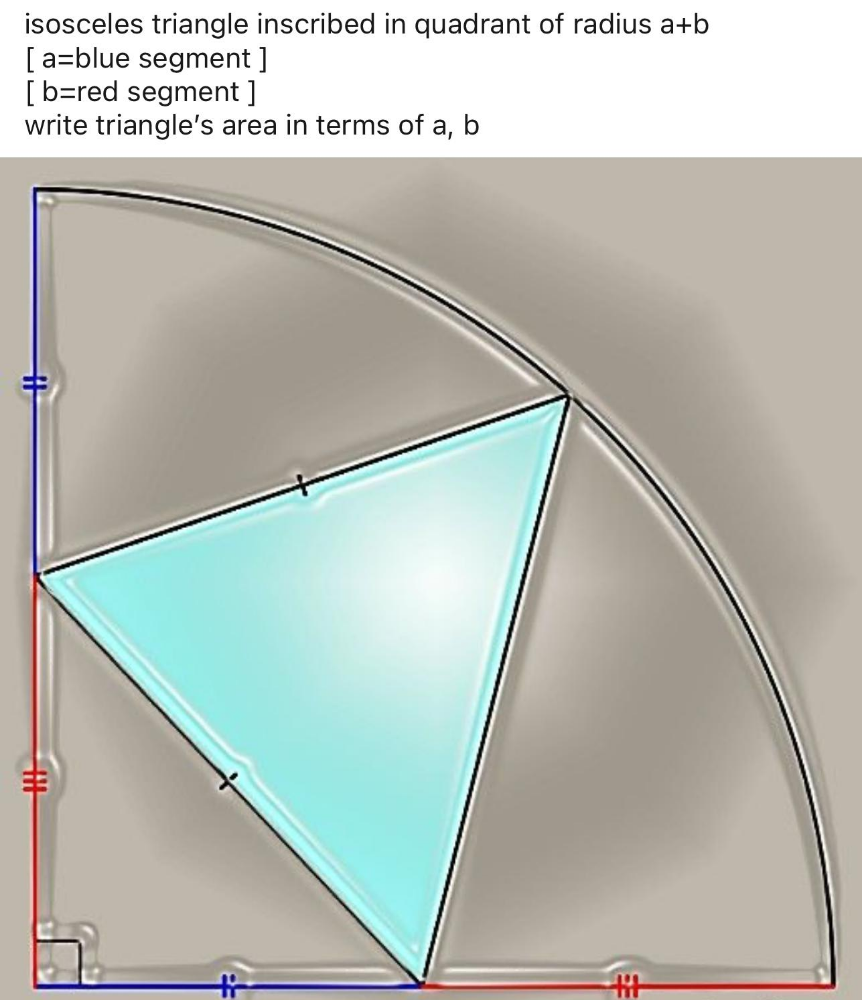
Answered by mr W last updated on 18/Jun/23
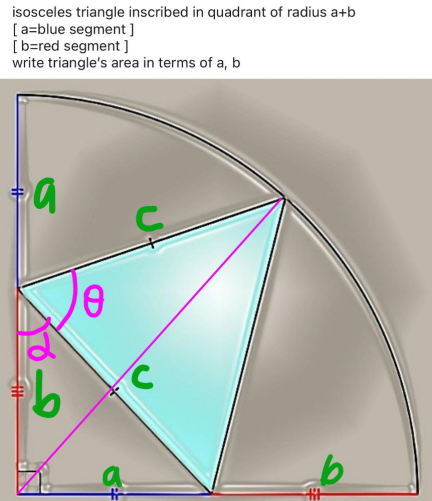
Commented by mr W last updated on 18/Jun/23
![c=(√(a^2 +b^2 )) R=a+b R^2 =b^2 +c^2 −2bc cos (α+θ) a^2 +b^2 +2ab=b^2 +a^2 +b^2 −2b(√(a^2 +b^2 )) cos (α+θ) b−2a=2(√(a^2 +b^2 )) cos (α+θ) b−2a=2(√(a^2 +b^2 )) (cos α cos θ−sin α sin θ) b−2a=2 (b cos θ−a sin θ) a sin θ−((2a−b)/2)=b cos θ a^2 sin^2 θ−(2a−b)a sin θ+(((2a−b)^2 )/4)=b^2 −b^2 sin^2 θ (a^2 +b^2 ) sin^2 θ−(2a−b)a sin θ+((4a^2 −4ab−3b^2 )/4)=0 sin θ=(1/(2(a^2 +b^2 )))[a(2a−b)+(√(a^2 (2a−b)^2 −(a^2 +b^2 )(4a^2 −4ab−3b^2 )))] Area=((c^2 sin θ)/2)=(1/4)[a(2a−b)+b(√(4a(2a−b)−b^2 ))]](Q193701.png)
$${c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${R}={a}+{b} \\ $$$${R}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\:\mathrm{cos}\:\left(\alpha+\theta\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}={b}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{b}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\mathrm{cos}\:\left(\alpha+\theta\right) \\ $$$${b}−\mathrm{2}{a}=\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\mathrm{cos}\:\left(\alpha+\theta\right) \\ $$$${b}−\mathrm{2}{a}=\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\left(\mathrm{cos}\:\alpha\:\mathrm{cos}\:\theta−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\theta\right) \\ $$$${b}−\mathrm{2}{a}=\mathrm{2}\:\left({b}\:\mathrm{cos}\:\theta−{a}\:\mathrm{sin}\:\theta\right) \\ $$$${a}\:\mathrm{sin}\:\theta−\frac{\mathrm{2}{a}−{b}}{\mathrm{2}}={b}\:\mathrm{cos}\:\theta \\ $$$${a}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta−\left(\mathrm{2}{a}−{b}\right){a}\:\mathrm{sin}\:\theta+\frac{\left(\mathrm{2}{a}−{b}\right)^{\mathrm{2}} }{\mathrm{4}}={b}^{\mathrm{2}} −{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$$\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\:\mathrm{sin}^{\mathrm{2}} \:\theta−\left(\mathrm{2}{a}−{b}\right){a}\:\mathrm{sin}\:\theta+\frac{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{ab}−\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\left.\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}\left[{a}\left(\mathrm{2}{a}−{b}\right)+\sqrt{{a}^{\mathrm{2}} \left(\mathrm{2}{a}−{b}\right)^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{ab}−\mathrm{3}{b}^{\mathrm{2}} \right.}\right)\right] \\ $$$${Area}=\frac{{c}^{\mathrm{2}} \:\mathrm{sin}\:\theta}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}}\left[{a}\left(\mathrm{2}{a}−{b}\right)+{b}\sqrt{\mathrm{4}{a}\left(\mathrm{2}{a}−{b}\right)−{b}^{\mathrm{2}} }\right] \\ $$
Commented by Rupesh123 last updated on 18/Jun/23
[1] check last two lines (1/2 ? --> 1/4 ) [2] simplify last radical
Commented by Mingma last updated on 18/Jun/23
It's been a while sir! Neat work!
Commented by Rupesh123 last updated on 18/Jun/23
Perfect ��
Commented by ajfour last updated on 20/Jun/23

$${P}\left({r}\mathrm{cos}\:\phi,\:{r}\mathrm{sin}\:\phi\right) \\ $$$${r}={a}+{b} \\ $$$${r}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi+\left({r}\mathrm{sin}\:\phi−{b}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{2}{ab}+{b}^{\mathrm{2}} =\mathrm{2}{br}\mathrm{sin}\:\phi \\ $$$$\&\:\:{altitude}\:{of}\:\bigtriangleup\:{is}\:\bot\:{to}\:{base},\:{so} \\ $$$$\frac{{r}\mathrm{sin}\:\phi}{{r}\mathrm{cos}\:\phi−{a}}=\frac{{a}+{r}\mathrm{cos}\:\phi}{\mathrm{2}{b}−{r}\mathrm{sin}\:\phi} \\ $$$$\Rightarrow\:\:\mathrm{2}{br}\mathrm{sin}\:\phi={r}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$${consider}\:\:\frac{{x}}{{a}}+\frac{{y}}{{b}}=\mathrm{1} \\ $$$${or}\:\:\:{bx}+{ay}−{ab}=\mathrm{0} \\ $$$${let}\:\:\:{h}=\frac{\mid{br}\mathrm{cos}\:\phi+{ar}\mathrm{sin}\:\phi−{ab}\mid}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${r}\mathrm{sin}\:\phi={a}+\frac{{b}}{\mathrm{2}} \\ $$$${h}=\frac{\mid{b}\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −\left({a}+\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} }+{a}^{\mathrm{2}} −\frac{{ab}}{\mathrm{2}}\mid}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\bigtriangleup=\frac{{ch}}{\mathrm{2}} \\ $$$$=\frac{{b}^{\mathrm{2}} }{\mathrm{2}}\mid\sqrt{\frac{\mathrm{3}}{\mathrm{4}}+\frac{{a}}{{b}}}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\frac{{a}}{\mathrm{2}{b}}\mid \\ $$
