
Question Number 193596 by Mingma last updated on 17/Jun/23
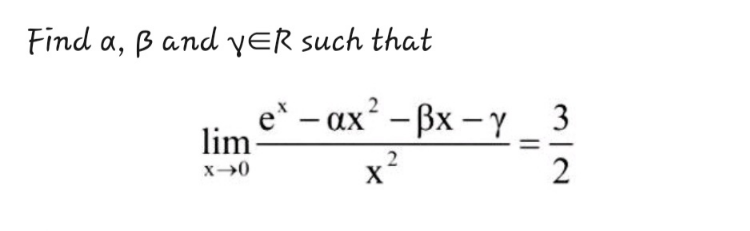
Answered by cortano12 last updated on 17/Jun/23
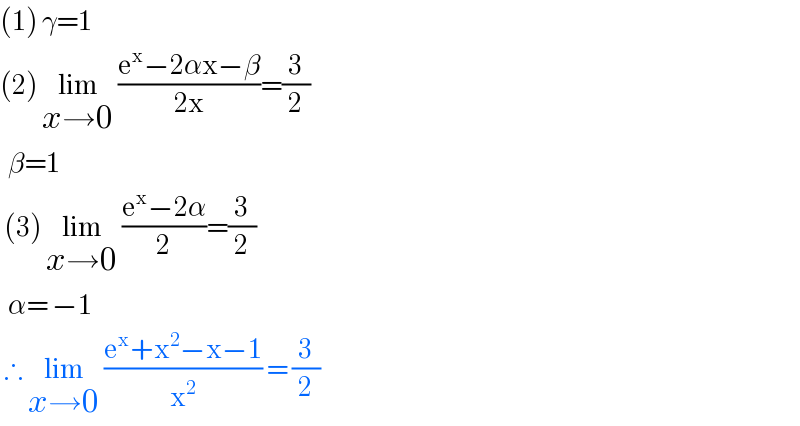
$$\left(\mathrm{1}\right)\:\gamma=\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{2}\alpha\mathrm{x}−\beta}{\mathrm{2x}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\beta=\mathrm{1}\: \\ $$$$\:\left(\mathrm{3}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{2}\alpha}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\alpha=\:−\mathrm{1} \\ $$$$\:\therefore\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by Mingma last updated on 17/Jun/23
Perfect ��
Answered by mnjuly1970 last updated on 17/Jun/23
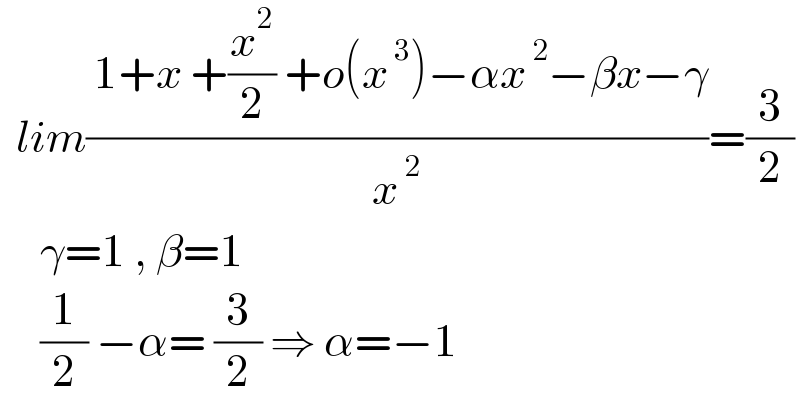
$$\:\:{lim}\frac{\:\mathrm{1}+{x}\:+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({x}^{\:\mathrm{3}} \right)−\alpha{x}^{\:\mathrm{2}} −\beta{x}−\gamma}{{x}^{\:\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\gamma=\mathrm{1}\:,\:\beta=\mathrm{1} \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:−\alpha=\:\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow\:\alpha=−\mathrm{1} \\ $$
