
Question Number 193435 by Mingma last updated on 14/Jun/23
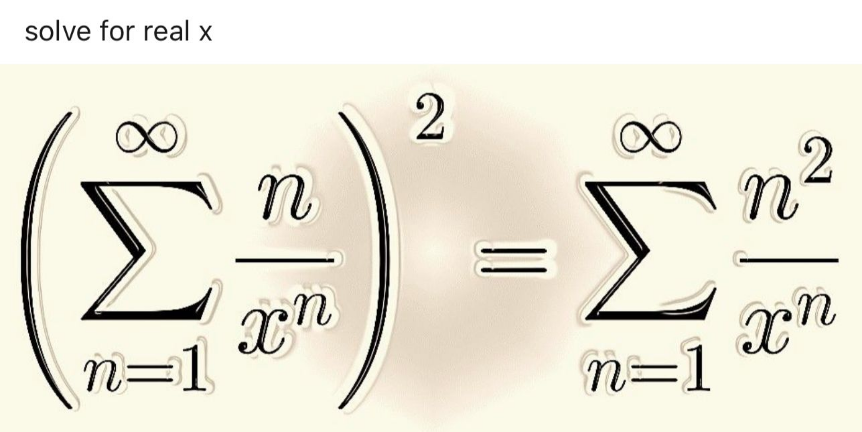
Commented by maths_plus last updated on 14/Jun/23

$$\mathrm{i}\:\mathrm{want}\:\mathrm{to}\:\mathrm{known}\:... \\ $$
Answered by qaz last updated on 14/Jun/23
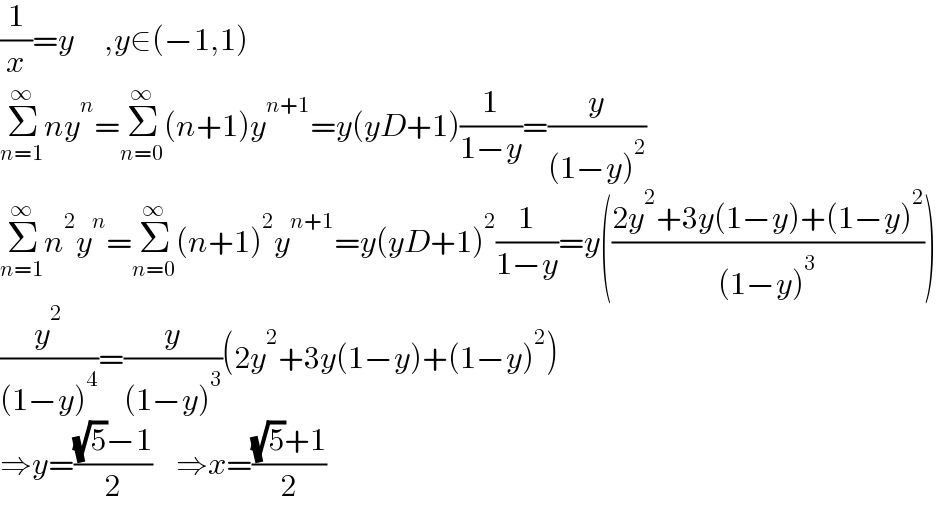
$$\frac{\mathrm{1}}{{x}}={y}\:\:\:\:\:,{y}\in\left(−\mathrm{1},\mathrm{1}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{ny}^{{n}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right){y}^{{n}+\mathrm{1}} ={y}\left({yD}+\mathrm{1}\right)\frac{\mathrm{1}}{\mathrm{1}−{y}}=\frac{{y}}{\left(\mathrm{1}−{y}\right)^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{\mathrm{2}} {y}^{{n}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right)^{\mathrm{2}} {y}^{{n}+\mathrm{1}} ={y}\left({yD}+\mathrm{1}\right)^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{1}−{y}}={y}\left(\frac{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{3}{y}\left(\mathrm{1}−{y}\right)+\left(\mathrm{1}−{y}\right)^{\mathrm{2}} }{\left(\mathrm{1}−{y}\right)^{\mathrm{3}} }\right) \\ $$$$\frac{{y}^{\mathrm{2}} }{\left(\mathrm{1}−{y}\right)^{\mathrm{4}} }=\frac{{y}}{\left(\mathrm{1}−{y}\right)^{\mathrm{3}} }\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{3}{y}\left(\mathrm{1}−{y}\right)+\left(\mathrm{1}−{y}\right)^{\mathrm{2}} \right) \\ $$$$\Rightarrow{y}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\:\:\:\:\Rightarrow{x}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Mingma last updated on 14/Jun/23
Perfect ��
