Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 193414 by mokys last updated on 13/Jun/23

Answered by deleteduser1 last updated on 13/Jun/23

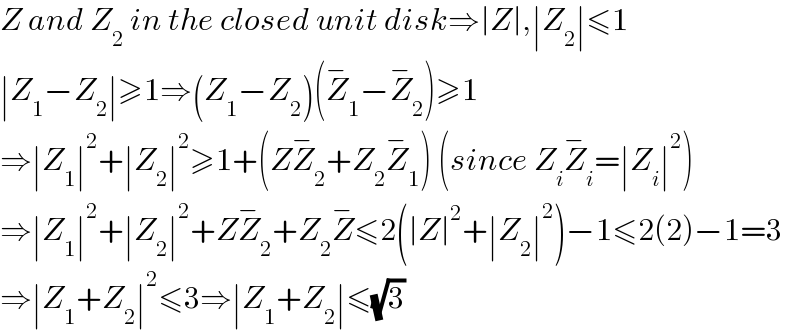
Z and Z_2 in the closed unit disk⇒∣Z∣,∣Z_2 ∣≤1 ∣Z_1 −Z_2 ∣≥1⇒(Z_1 −Z_2 )(Z_1 ^− −Z_2 ^− )≥1 ⇒∣Z_1 ∣^2 +∣Z_2 ∣^2 ≥1+(ZZ_2 ^− +Z_2 Z_1 ^− ) (since Z_i Z_i ^− =∣Z_i ∣^2 ) ⇒∣Z_1 ∣^2 +∣Z_2 ∣^2 +ZZ_2 ^− +Z_2 Z^− ≤2(∣Z∣^2 +∣Z_2 ∣^2 )−1≤2(2)−1=3 ⇒∣Z_1 +Z_2 ∣^2 ≤3⇒∣Z_1 +Z_2 ∣≤(√3)

$${Z}\:{and}\:{Z}_{\mathrm{2}} \:{in}\:{the}\:{closed}\:{unit}\:{disk}\Rightarrow\mid{Z}\mid,\mid{Z}_{\mathrm{2}} \mid\leqslant\mathrm{1} \\ $$$$\mid{Z}_{\mathrm{1}} −{Z}_{\mathrm{2}} \mid\geqslant\mathrm{1}\Rightarrow\left({Z}_{\mathrm{1}} −{Z}_{\mathrm{2}} \right)\left(\overset{−} {{Z}}_{\mathrm{1}} −\overset{−} {{Z}}_{\mathrm{2}} \right)\geqslant\mathrm{1} \\ $$$$\Rightarrow\mid{Z}_{\mathrm{1}} \mid^{\mathrm{2}} +\mid{Z}_{\mathrm{2}} \mid^{\mathrm{2}} \geqslant\mathrm{1}+\left({Z}\overset{−} {{Z}}_{\mathrm{2}} +{Z}_{\mathrm{2}} \overset{−} {{Z}}_{\mathrm{1}} \right)\:\left({since}\:{Z}_{{i}} \overset{−} {{Z}}_{{i}} =\mid{Z}_{{i}} \mid^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mid{Z}_{\mathrm{1}} \mid^{\mathrm{2}} +\mid{Z}_{\mathrm{2}} \mid^{\mathrm{2}} +{Z}\overset{−} {{Z}}_{\mathrm{2}} +{Z}_{\mathrm{2}} \overset{−} {{Z}}\leqslant\mathrm{2}\left(\mid{Z}\mid^{\mathrm{2}} +\mid{Z}_{\mathrm{2}} \mid^{\mathrm{2}} \right)−\mathrm{1}\leqslant\mathrm{2}\left(\mathrm{2}\right)−\mathrm{1}=\mathrm{3} \\ $$$$\Rightarrow\mid{Z}_{\mathrm{1}} +{Z}_{\mathrm{2}} \mid^{\mathrm{2}} \leqslant\mathrm{3}\Rightarrow\mid{Z}_{\mathrm{1}} +{Z}_{\mathrm{2}} \mid\leqslant\sqrt{\mathrm{3}} \\ $$

Answered by witcher3 last updated on 13/Jun/23

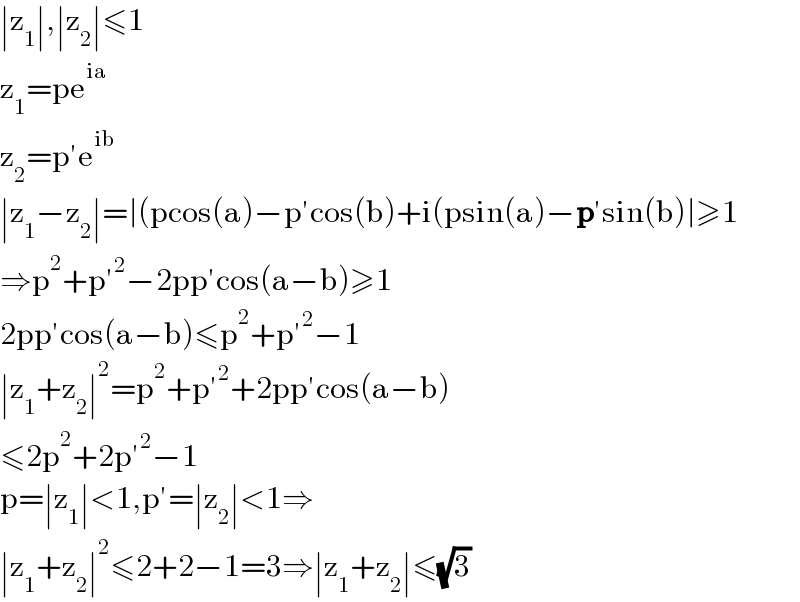
∣z_1 ∣,∣z_2 ∣≤1 z_1 =pe^(ia) z_2 =p′e^(ib) ∣z_1 −z_2 ∣=∣(pcos(a)−p′cos(b)+i(psin(a)−p′sin(b)∣≥1 ⇒p^2 +p′^2 −2pp′cos(a−b)≥1 2pp′cos(a−b)≤p^2 +p′^2 −1 ∣z_1 +z_2 ∣^2 =p^2 +p′^2 +2pp′cos(a−b) ≤2p^2 +2p′^2 −1 p=∣z_1 ∣<1,p′=∣z_2 ∣<1⇒ ∣z_1 +z_2 ∣^2 ≤2+2−1=3⇒∣z_1 +z_2 ∣≤(√3)

$$\mid\mathrm{z}_{\mathrm{1}} \mid,\mid\mathrm{z}_{\mathrm{2}} \mid\leqslant\mathrm{1} \\ $$$$\mathrm{z}_{\mathrm{1}} =\mathrm{pe}^{\mathrm{ia}} \\ $$$$\mathrm{z}_{\mathrm{2}} =\mathrm{p}'\mathrm{e}^{\mathrm{ib}} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} \mid=\mid\left(\mathrm{pcos}\left(\mathrm{a}\right)−\mathrm{p}'\mathrm{cos}\left(\mathrm{b}\right)+\mathrm{i}\left(\mathrm{psin}\left(\mathrm{a}\right)−\boldsymbol{\mathrm{p}}'\mathrm{sin}\left(\mathrm{b}\right)\mid\geqslant\mathrm{1}\right.\right. \\ $$$$\Rightarrow\mathrm{p}^{\mathrm{2}} +\mathrm{p}'^{\mathrm{2}} −\mathrm{2pp}'\mathrm{cos}\left(\mathrm{a}−\mathrm{b}\right)\geqslant\mathrm{1} \\ $$$$\mathrm{2pp}'\mathrm{cos}\left(\mathrm{a}−\mathrm{b}\right)\leqslant\mathrm{p}^{\mathrm{2}} +\mathrm{p}'^{\mathrm{2}} −\mathrm{1} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} +\mathrm{z}_{\mathrm{2}} \mid^{\mathrm{2}} =\mathrm{p}^{\mathrm{2}} +\mathrm{p}'^{\mathrm{2}} +\mathrm{2pp}'\mathrm{cos}\left(\mathrm{a}−\mathrm{b}\right) \\ $$$$\leqslant\mathrm{2p}^{\mathrm{2}} +\mathrm{2p}'^{\mathrm{2}} −\mathrm{1} \\ $$$$\mathrm{p}=\mid\mathrm{z}_{\mathrm{1}} \mid<\mathrm{1},\mathrm{p}'=\mid\mathrm{z}_{\mathrm{2}} \mid<\mathrm{1}\Rightarrow \\ $$$$\mid\mathrm{z}_{\mathrm{1}} +\mathrm{z}_{\mathrm{2}} \mid^{\mathrm{2}} \leqslant\mathrm{2}+\mathrm{2}−\mathrm{1}=\mathrm{3}\Rightarrow\mid\mathrm{z}_{\mathrm{1}} +\mathrm{z}_{\mathrm{2}} \mid\leqslant\sqrt{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com