
Question Number 192227 by sonukgindia last updated on 12/May/23
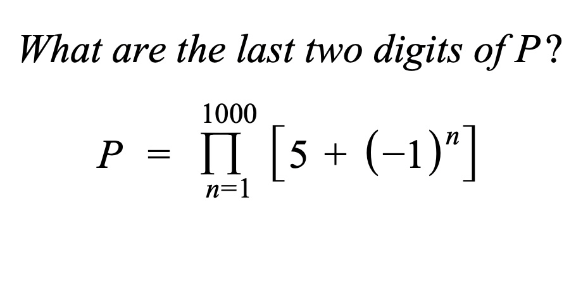
Answered by senestro last updated on 12/May/23

$$...\mathrm{76} \\ $$
Commented by text last updated on 12/May/23

$$...\mathrm{76} \\ $$
Answered by JDamian last updated on 13/May/23
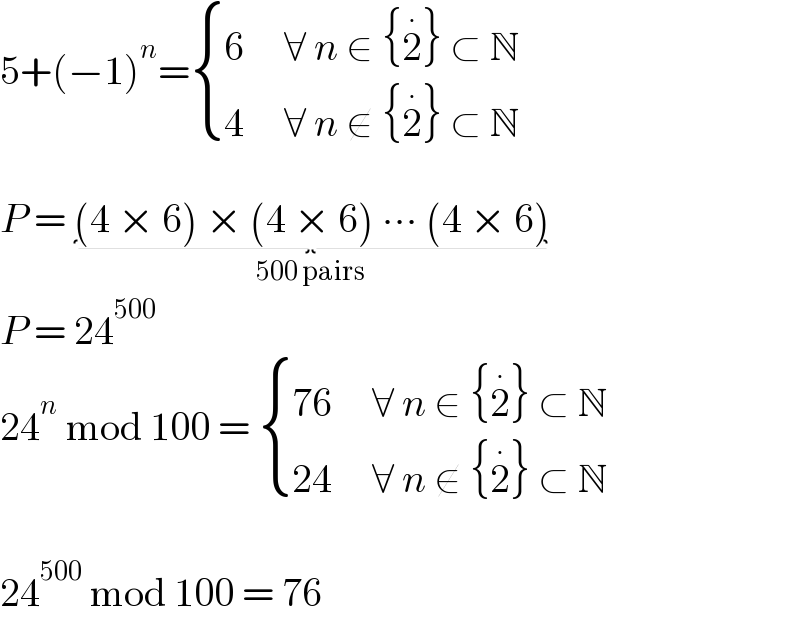
$$\mathrm{5}+\left(−\mathrm{1}\right)^{{n}} =\begin{cases}{\mathrm{6}\:\:\:\:\:\forall\:{n}\:\in\:\left\{\overset{\centerdot} {\mathrm{2}}\right\}\:\subset\:\mathbb{N}}\\{\mathrm{4}\:\:\:\:\:\forall\:{n}\:\notin\:\left\{\overset{\centerdot} {\mathrm{2}}\right\}\:\subset\:\mathbb{N}}\end{cases} \\ $$$$ \\ $$$${P}\:=\:\underset{\mathrm{500}\:\mathrm{pairs}} {\underbrace{\left(\mathrm{4}\:×\:\mathrm{6}\right)\:×\:\left(\mathrm{4}\:×\:\mathrm{6}\right)\:\centerdot\centerdot\centerdot\:\left(\mathrm{4}\:×\:\mathrm{6}\right)}} \\ $$$${P}\:=\:\mathrm{24}^{\mathrm{500}} \\ $$$$\mathrm{24}^{{n}} \:\mathrm{mod}\:\mathrm{100}\:=\:\begin{cases}{\mathrm{76}\:\:\:\:\:\forall\:{n}\:\in\:\left\{\overset{\centerdot} {\mathrm{2}}\right\}\:\subset\:\mathbb{N}}\\{\mathrm{24}\:\:\:\:\:\forall\:{n}\:\notin\:\left\{\overset{\centerdot} {\mathrm{2}}\right\}\:\subset\:\mathbb{N}}\end{cases} \\ $$$$ \\ $$$$\mathrm{24}^{\mathrm{500}} \:\mathrm{mod}\:\mathrm{100}\:=\:\mathrm{76} \\ $$
