
Question Number 191753 by Abdullahrussell last updated on 30/Apr/23
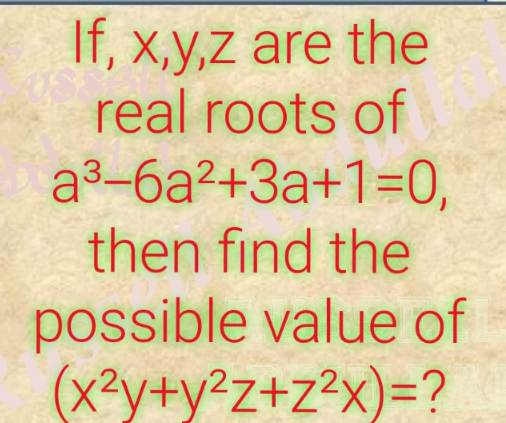
Answered by Frix last updated on 30/Apr/23
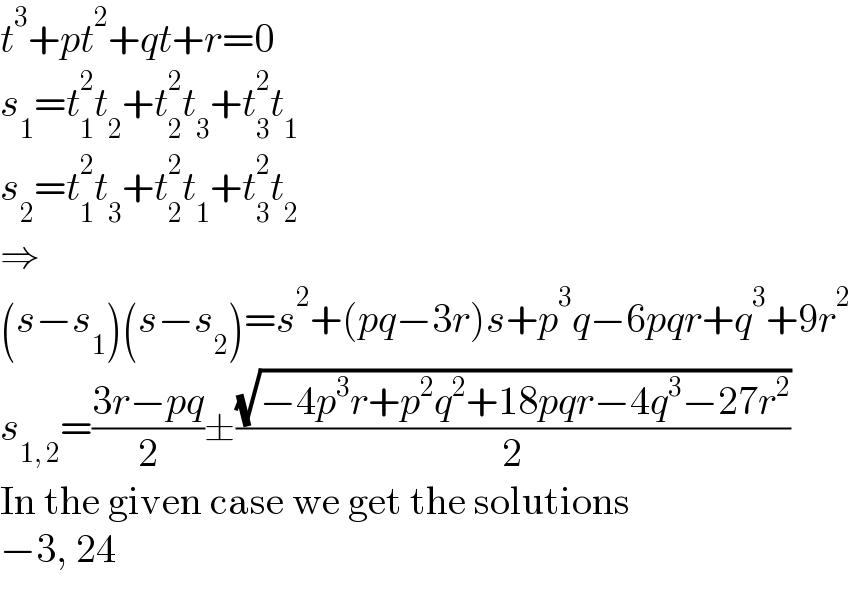
$${t}^{\mathrm{3}} +{pt}^{\mathrm{2}} +{qt}+{r}=\mathrm{0} \\ $$$${s}_{\mathrm{1}} ={t}_{\mathrm{1}} ^{\mathrm{2}} {t}_{\mathrm{2}} +{t}_{\mathrm{2}} ^{\mathrm{2}} {t}_{\mathrm{3}} +{t}_{\mathrm{3}} ^{\mathrm{2}} {t}_{\mathrm{1}} \\ $$$${s}_{\mathrm{2}} ={t}_{\mathrm{1}} ^{\mathrm{2}} {t}_{\mathrm{3}} +{t}_{\mathrm{2}} ^{\mathrm{2}} {t}_{\mathrm{1}} +{t}_{\mathrm{3}} ^{\mathrm{2}} {t}_{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\left({s}−{s}_{\mathrm{1}} \right)\left({s}−{s}_{\mathrm{2}} \right)={s}^{\mathrm{2}} +\left({pq}−\mathrm{3}{r}\right){s}+{p}^{\mathrm{3}} {q}−\mathrm{6}{pqr}+{q}^{\mathrm{3}} +\mathrm{9}{r}^{\mathrm{2}} \\ $$$${s}_{\mathrm{1},\:\mathrm{2}} =\frac{\mathrm{3}{r}−{pq}}{\mathrm{2}}\pm\frac{\sqrt{−\mathrm{4}{p}^{\mathrm{3}} {r}+{p}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{18}{pqr}−\mathrm{4}{q}^{\mathrm{3}} −\mathrm{27}{r}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\mathrm{In}\:\mathrm{the}\:\mathrm{given}\:\mathrm{case}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{solutions} \\ $$$$−\mathrm{3},\:\mathrm{24} \\ $$
