
Question Number 191706 by BaliramKumar last updated on 29/Apr/23
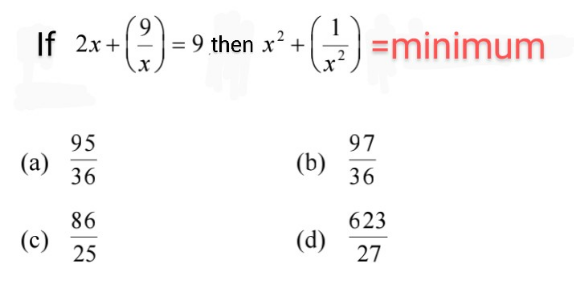
Answered by Skabetix last updated on 29/Apr/23

$$\rightarrow\left({b}\right)\:\frac{\mathrm{97}}{\mathrm{36}} \\ $$
Answered by Skabetix last updated on 29/Apr/23
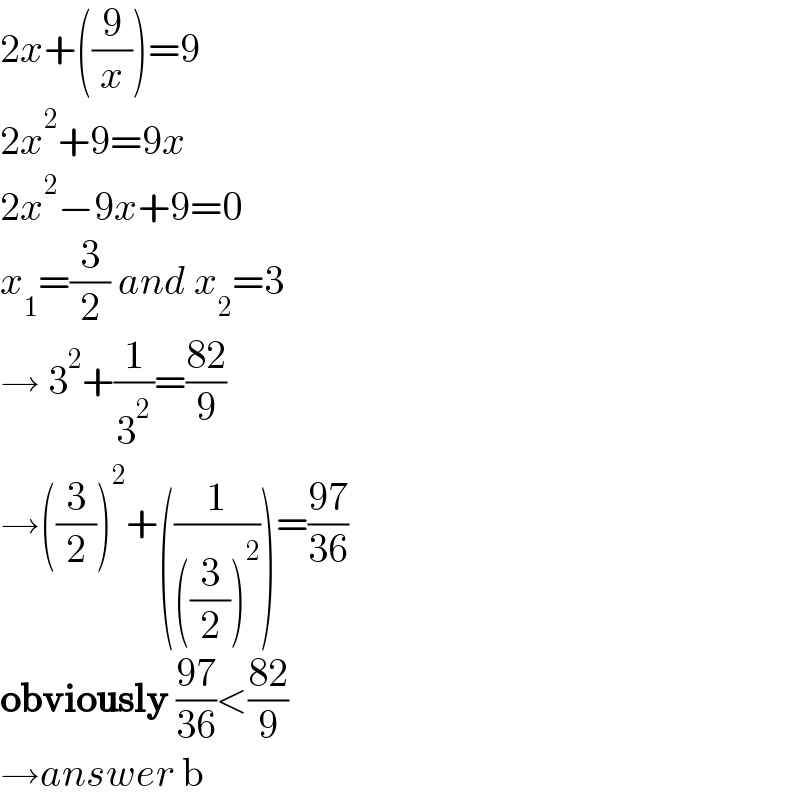
$$\mathrm{2}{x}+\left(\frac{\mathrm{9}}{{x}}\right)=\mathrm{9} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{9}=\mathrm{9}{x} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{9}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{2}}\:{and}\:{x}_{\mathrm{2}} =\mathrm{3} \\ $$$$\rightarrow\:\mathrm{3}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }=\frac{\mathrm{82}}{\mathrm{9}} \\ $$$$\rightarrow\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }\right)=\frac{\mathrm{97}}{\mathrm{36}} \\ $$$$\boldsymbol{\mathrm{obviously}}\:\frac{\mathrm{97}}{\mathrm{36}}<\frac{\mathrm{82}}{\mathrm{9}} \\ $$$$\rightarrow{answer}\:\mathrm{b} \\ $$
Commented by BaliramKumar last updated on 29/Apr/23

$$\mathrm{Thanks} \\ $$
