
Question Number 191621 by Noorzai last updated on 27/Apr/23
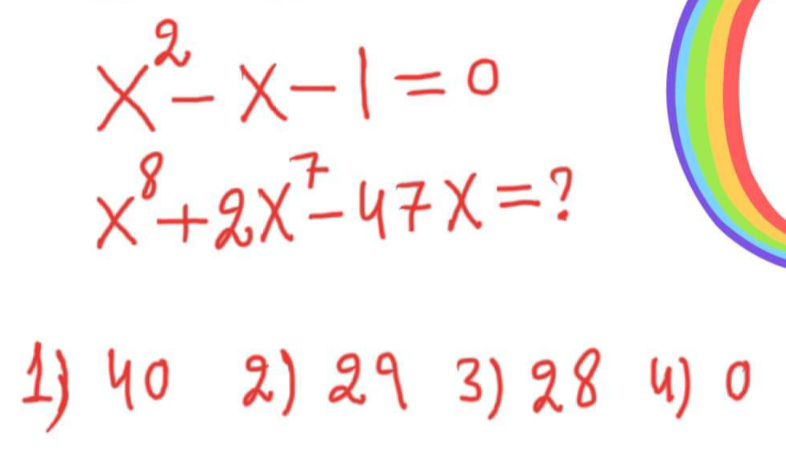
Answered by gatocomcirrose last updated on 27/Apr/23
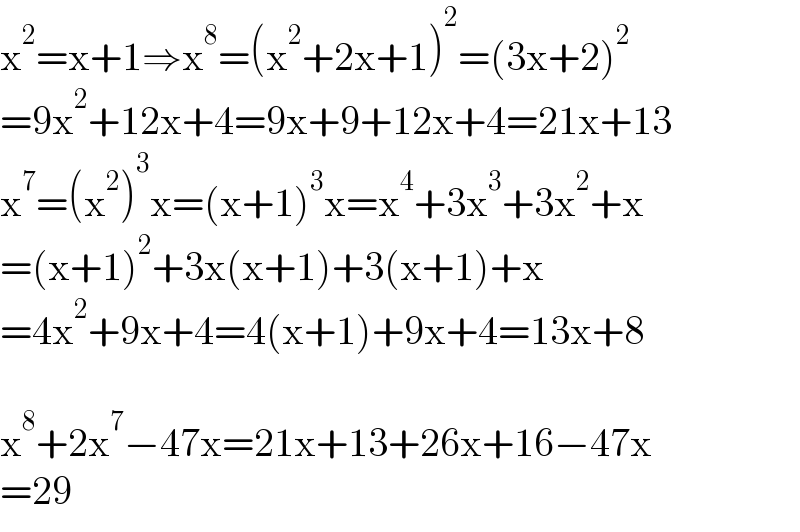
$$\mathrm{x}^{\mathrm{2}} =\mathrm{x}+\mathrm{1}\Rightarrow\mathrm{x}^{\mathrm{8}} =\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{3x}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$=\mathrm{9x}^{\mathrm{2}} +\mathrm{12x}+\mathrm{4}=\mathrm{9x}+\mathrm{9}+\mathrm{12x}+\mathrm{4}=\mathrm{21x}+\mathrm{13} \\ $$$$\mathrm{x}^{\mathrm{7}} =\left(\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} \mathrm{x}=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \mathrm{x}=\mathrm{x}^{\mathrm{4}} +\mathrm{3x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{x} \\ $$$$=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3x}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{3}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{x} \\ $$$$=\mathrm{4x}^{\mathrm{2}} +\mathrm{9x}+\mathrm{4}=\mathrm{4}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{9x}+\mathrm{4}=\mathrm{13x}+\mathrm{8} \\ $$$$ \\ $$$$\mathrm{x}^{\mathrm{8}} +\mathrm{2x}^{\mathrm{7}} −\mathrm{47x}=\mathrm{21x}+\mathrm{13}+\mathrm{26x}+\mathrm{16}−\mathrm{47x} \\ $$$$=\mathrm{29} \\ $$
Commented by Noorzai last updated on 28/Apr/23
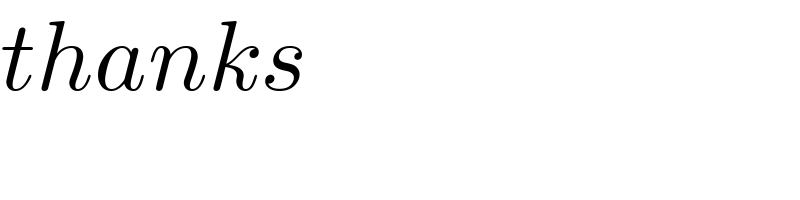
$${thanks} \\ $$
Answered by manxsol last updated on 28/Apr/23
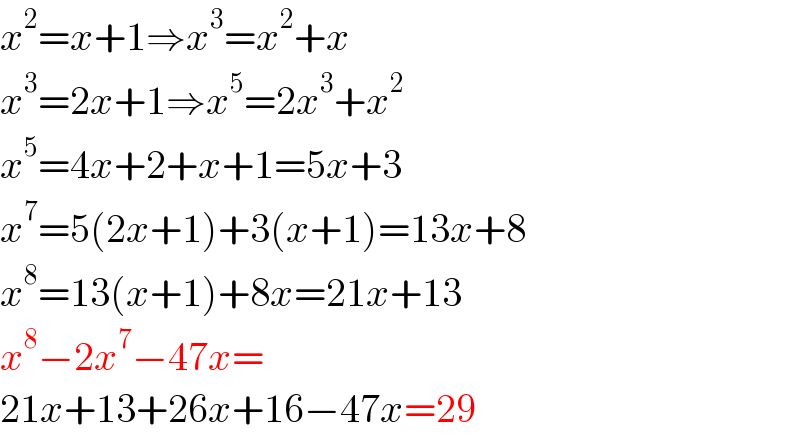
$${x}^{\mathrm{2}} ={x}+\mathrm{1}\Rightarrow{x}^{\mathrm{3}} ={x}^{\mathrm{2}} +{x} \\ $$$${x}^{\mathrm{3}} =\mathrm{2}{x}+\mathrm{1}\Rightarrow{x}^{\mathrm{5}} =\mathrm{2}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{5}} =\mathrm{4}{x}+\mathrm{2}+{x}+\mathrm{1}=\mathrm{5}{x}+\mathrm{3} \\ $$$${x}^{\mathrm{7}} =\mathrm{5}\left(\mathrm{2}{x}+\mathrm{1}\right)+\mathrm{3}\left({x}+\mathrm{1}\right)=\mathrm{13}{x}+\mathrm{8} \\ $$$${x}^{\mathrm{8}} =\mathrm{13}\left({x}+\mathrm{1}\right)+\mathrm{8}{x}=\mathrm{21}{x}+\mathrm{13} \\ $$$${x}^{\mathrm{8}} −\mathrm{2}{x}^{\mathrm{7}} −\mathrm{47}{x}= \\ $$$$\mathrm{21}{x}+\mathrm{13}+\mathrm{26}{x}+\mathrm{16}−\mathrm{47}{x}=\mathrm{29} \\ $$
