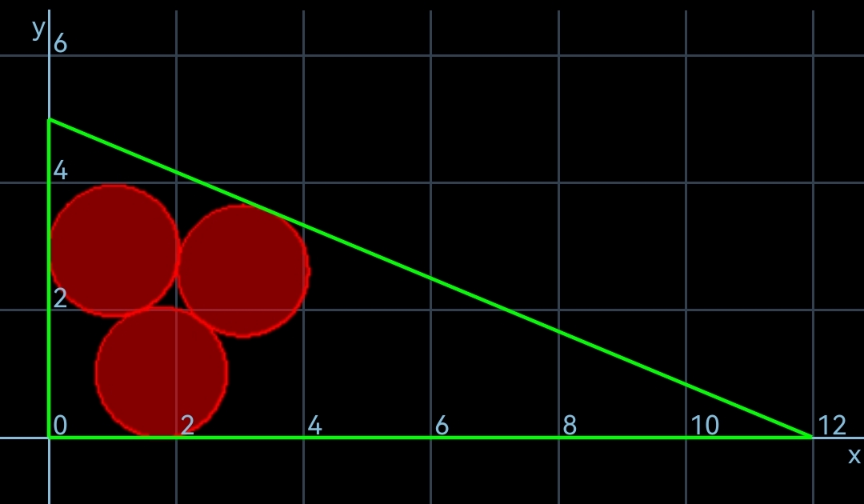
Question Number 191305 by Mingma last updated on 22/Apr/23
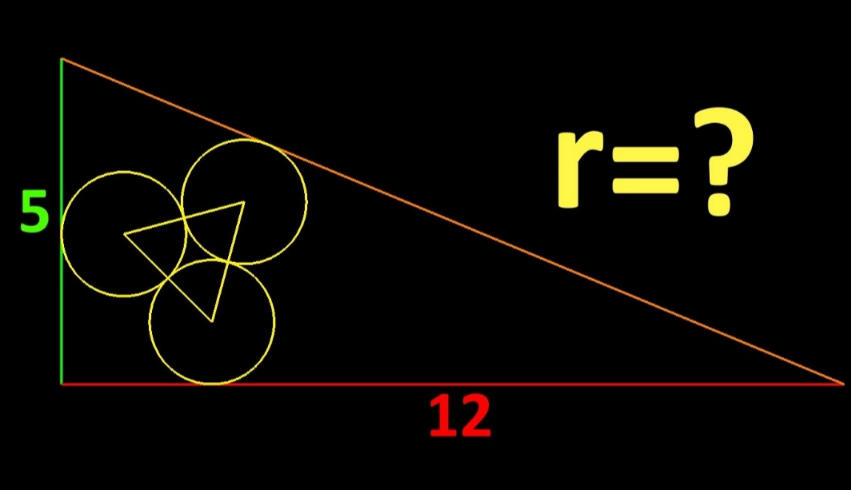
Commented by mr W last updated on 22/Apr/23

$${there}\:{is}\:{no}\:{unique}\:{solution}.\:{but}\:{there} \\ $$$${is}\:{a}\:{r}_{{min}} . \\ $$
Answered by mr W last updated on 23/Apr/23
Commented by mr W last updated on 23/Apr/23
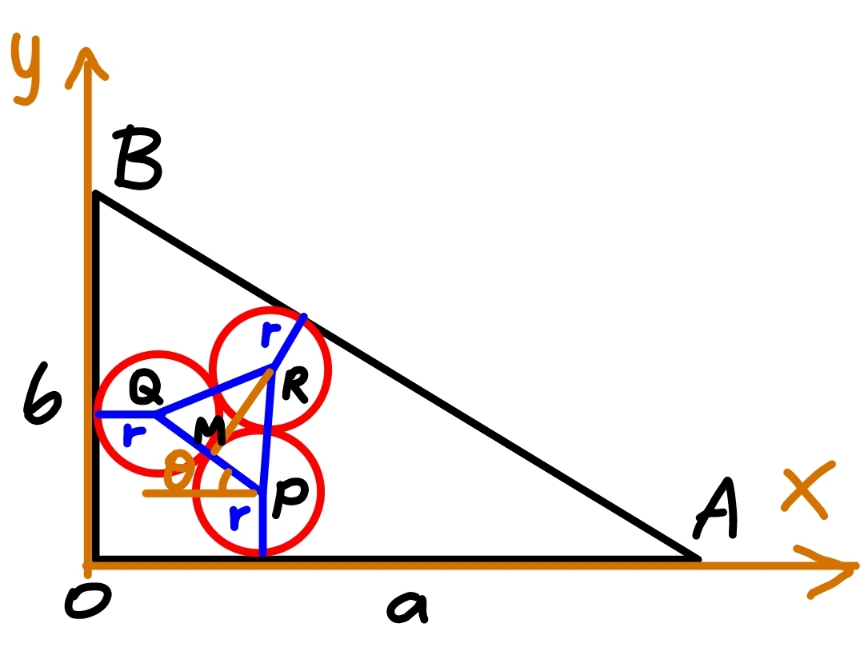
![OA=a=12 OB=b=5 say P(p,r), Q(r,q) p=r+2r cos θ q=r+2r sin θ M=mid point of PQ M(((p+r)/2),((q+r)/2))=[(1+cos θ)r, (1+sin θ)r] QM=(√3)r x_R =(1+cos θ+(√3) sin θ)r y_R =(1+sin θ+(√3) cos θ)r eqn. of AB: (x/a)+(y/b)=1 ⇒bx+ay−ab=0 distance from R to AB is r: ((∣b(1+cos θ+(√3) sin θ)r+a(1+sin θ+(√3) cos θ)r−ab∣)/( (√(a^2 +b^2 ))))=r r=((ab)/(a+b+(√(a^2 +b^2 ))+(a+(√3)b)sin θ+((√3)a+b)cos θ)) r=((ab)/(a+b+(√(a^2 +b^2 ))+2(√(a^2 +b^2 +(√3)ab)) sin (θ+tan^(−1) (((√3)a+b)/(a+(√3)b))))) at θ+tan^(−1) (((√3)a+b)/(a+(√3)b))=(π/2), i.e. θ=(π/2)−tan^(−1) (((√3)a+b)/(a+(√3)b)) : r_(min) =((ab)/(a+b+(√(a^2 +b^2 ))+2(√(a^2 +b^2 +(√3)ab)))) with a=12, b=5: r_(min) =((30)/(15+(√(169+60(√3)))))≈0.952](Q191319.png)
$${OA}={a}=\mathrm{12} \\ $$$${OB}={b}=\mathrm{5} \\ $$$${say}\:{P}\left({p},{r}\right),\:{Q}\left({r},{q}\right) \\ $$$${p}={r}+\mathrm{2}{r}\:\mathrm{cos}\:\theta \\ $$$${q}={r}+\mathrm{2}{r}\:\mathrm{sin}\:\theta \\ $$$${M}={mid}\:{point}\:{of}\:{PQ} \\ $$$${M}\left(\frac{{p}+{r}}{\mathrm{2}},\frac{{q}+{r}}{\mathrm{2}}\right)=\left[\left(\mathrm{1}+\mathrm{cos}\:\theta\right){r},\:\left(\mathrm{1}+\mathrm{sin}\:\theta\right){r}\right] \\ $$$${QM}=\sqrt{\mathrm{3}}{r} \\ $$$${x}_{{R}} =\left(\mathrm{1}+\mathrm{cos}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right){r} \\ $$$${y}_{{R}} =\left(\mathrm{1}+\mathrm{sin}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\theta\right){r} \\ $$$${eqn}.\:{of}\:{AB}: \\ $$$$\frac{{x}}{{a}}+\frac{{y}}{{b}}=\mathrm{1}\:\Rightarrow{bx}+{ay}−{ab}=\mathrm{0} \\ $$$${distance}\:{from}\:{R}\:{to}\:{AB}\:{is}\:{r}: \\ $$$$\frac{\mid{b}\left(\mathrm{1}+\mathrm{cos}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right){r}+{a}\left(\mathrm{1}+\mathrm{sin}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\theta\right){r}−{ab}\mid}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}={r} \\ $$$${r}=\frac{{ab}}{{a}+{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\left({a}+\sqrt{\mathrm{3}}{b}\right)\mathrm{sin}\:\theta+\left(\sqrt{\mathrm{3}}{a}+{b}\right)\mathrm{cos}\:\theta} \\ $$$${r}=\frac{{ab}}{{a}+{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\mathrm{3}}{ab}}\:\mathrm{sin}\:\left(\theta+\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}{a}+{b}}{{a}+\sqrt{\mathrm{3}}{b}}\right)} \\ $$$${at}\:\theta+\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}{a}+{b}}{{a}+\sqrt{\mathrm{3}}{b}}=\frac{\pi}{\mathrm{2}},\:{i}.{e}.\:\theta=\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}{a}+{b}}{{a}+\sqrt{\mathrm{3}}{b}}\:: \\ $$$${r}_{{min}} =\frac{{ab}}{{a}+{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\mathrm{3}}{ab}}} \\ $$$${with}\:{a}=\mathrm{12},\:{b}=\mathrm{5}: \\ $$$${r}_{{min}} =\frac{\mathrm{30}}{\mathrm{15}+\sqrt{\mathrm{169}+\mathrm{60}\sqrt{\mathrm{3}}}}\approx\mathrm{0}.\mathrm{952} \\ $$
Commented by Mingma last updated on 23/Apr/23
Great Work, sir!
Commented by mr W last updated on 23/Apr/23

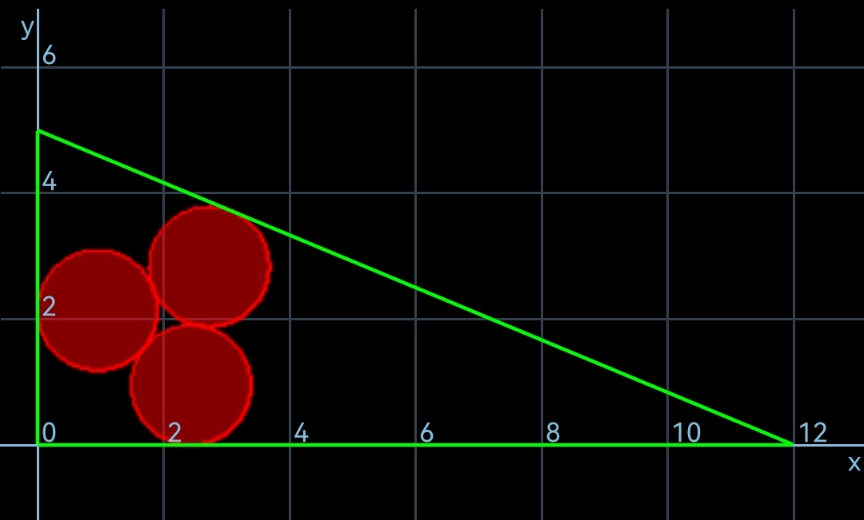
$${with}\:{r}_{{min}} : \\ $$
Commented by mr W last updated on 23/Apr/23
Commented by mr W last updated on 23/Apr/23
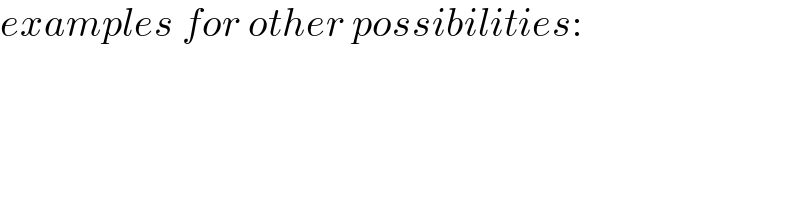
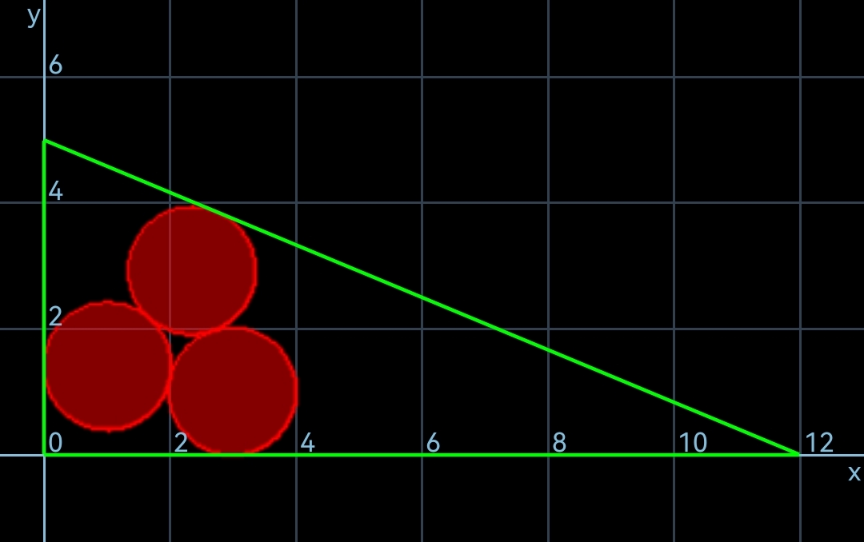
$${examples}\:{for}\:{other}\:{possibilities}: \\ $$
Commented by mr W last updated on 23/Apr/23
Commented by mr W last updated on 23/Apr/23