Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 191304 by Mingma last updated on 22/Apr/23

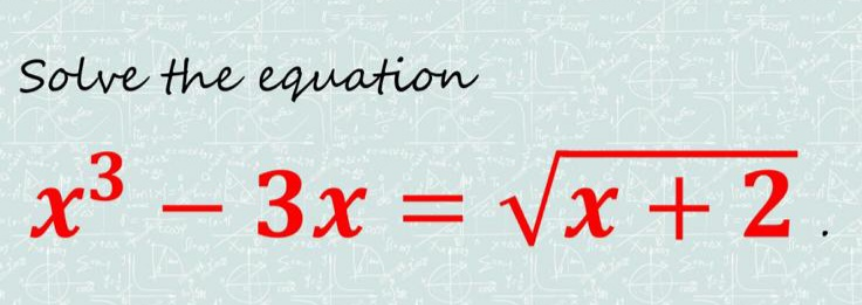
Answered by cortano12 last updated on 22/Apr/23

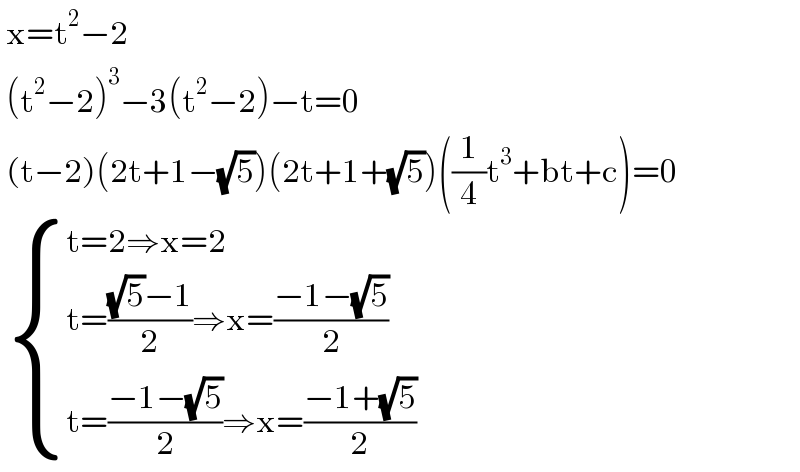
x=t^2 −2 (t^2 −2)^3 −3(t^2 −2)−t=0 (t−2)(2t+1−(√5))(2t+1+(√5))((1/4)t^3 +bt+c)=0 { ((t=2⇒x=2)),((t=(((√5)−1)/2)⇒x=((−1−(√5))/2))),((t=((−1−(√5))/2)⇒x=((−1+(√5))/2))) :}

$$\:\mathrm{x}=\mathrm{t}^{\mathrm{2}} −\mathrm{2}\: \\ $$$$\:\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{t}=\mathrm{0} \\ $$$$\:\left(\mathrm{t}−\mathrm{2}\right)\left(\mathrm{2t}+\mathrm{1}−\sqrt{\mathrm{5}}\right)\left(\mathrm{2t}+\mathrm{1}+\sqrt{\mathrm{5}}\right)\left(\frac{\mathrm{1}}{\mathrm{4}}\mathrm{t}^{\mathrm{3}} +\mathrm{bt}+\mathrm{c}\right)=\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{t}=\mathrm{2}\Rightarrow\mathrm{x}=\mathrm{2}}\\{\mathrm{t}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{x}=\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}}\\{\mathrm{t}=\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\Rightarrow\mathrm{x}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}\end{cases} \\ $$

Commented by Frix last updated on 22/Apr/23

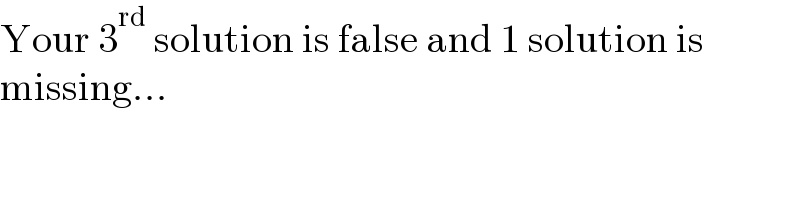
Your 3^(rd) solution is false and 1 solution is missing...

$$\mathrm{Your}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{solution}\:\mathrm{is}\:\mathrm{false}\:\mathrm{and}\:\mathrm{1}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{missing}... \\ $$

Answered by Frix last updated on 22/Apr/23

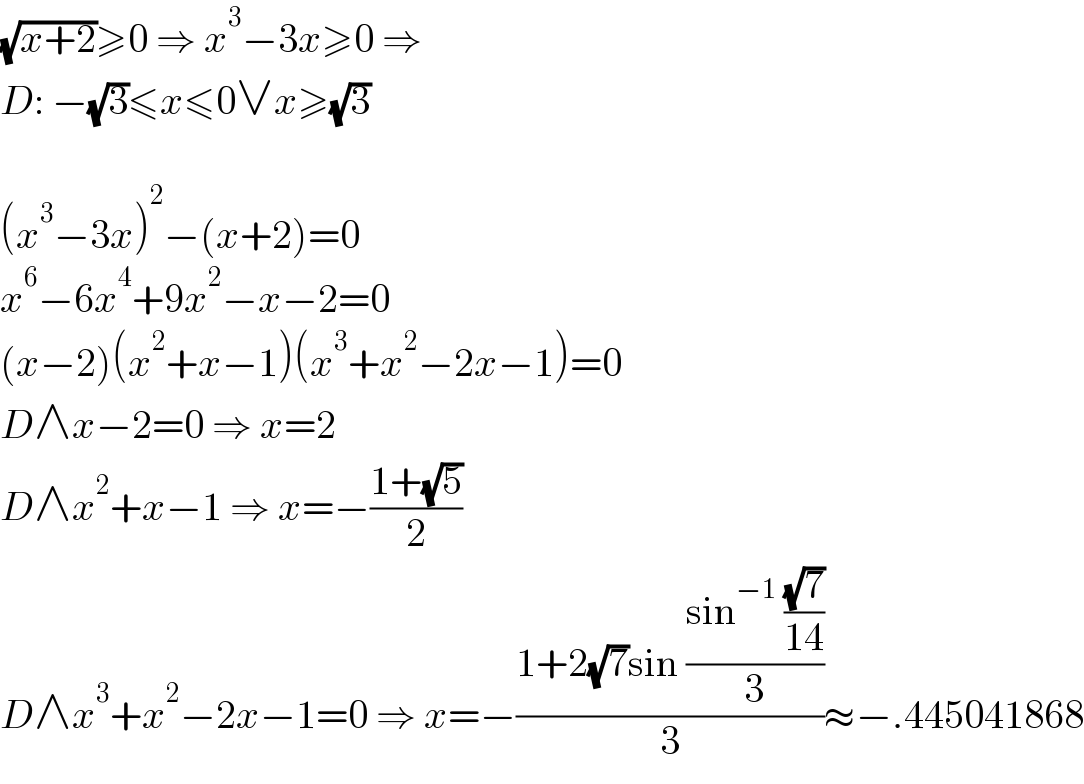
(√(x+2))≥0 ⇒ x^3 −3x≥0 ⇒ D: −(√3)≤x≤0∨x≥(√3) (x^3 −3x)^2 −(x+2)=0 x^6 −6x^4 +9x^2 −x−2=0 (x−2)(x^2 +x−1)(x^3 +x^2 −2x−1)=0 D∧x−2=0 ⇒ x=2 D∧x^2 +x−1 ⇒ x=−((1+(√5))/2) D∧x^3 +x^2 −2x−1=0 ⇒ x=−((1+2(√7)sin ((sin^(−1) ((√7)/(14)))/3))/3)≈−.445041868

$$\sqrt{{x}+\mathrm{2}}\geqslant\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{3}} −\mathrm{3}{x}\geqslant\mathrm{0}\:\Rightarrow \\ $$$${D}:\:−\sqrt{\mathrm{3}}\leqslant{x}\leqslant\mathrm{0}\vee{x}\geqslant\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$\left({x}^{\mathrm{3}} −\mathrm{3}{x}\right)^{\mathrm{2}} −\left({x}+\mathrm{2}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{6}} −\mathrm{6}{x}^{\mathrm{4}} +\mathrm{9}{x}^{\mathrm{2}} −{x}−\mathrm{2}=\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{1}\right)\left({x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${D}\wedge{x}−\mathrm{2}=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{2} \\ $$$${D}\wedge{x}^{\mathrm{2}} +{x}−\mathrm{1}\:\Rightarrow\:{x}=−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${D}\wedge{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}=\mathrm{0}\:\Rightarrow\:{x}=−\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{7}}\mathrm{sin}\:\frac{\mathrm{sin}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}}{\mathrm{3}}}{\mathrm{3}}\approx−.\mathrm{445041868} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com