Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 191275 by Mingma last updated on 22/Apr/23

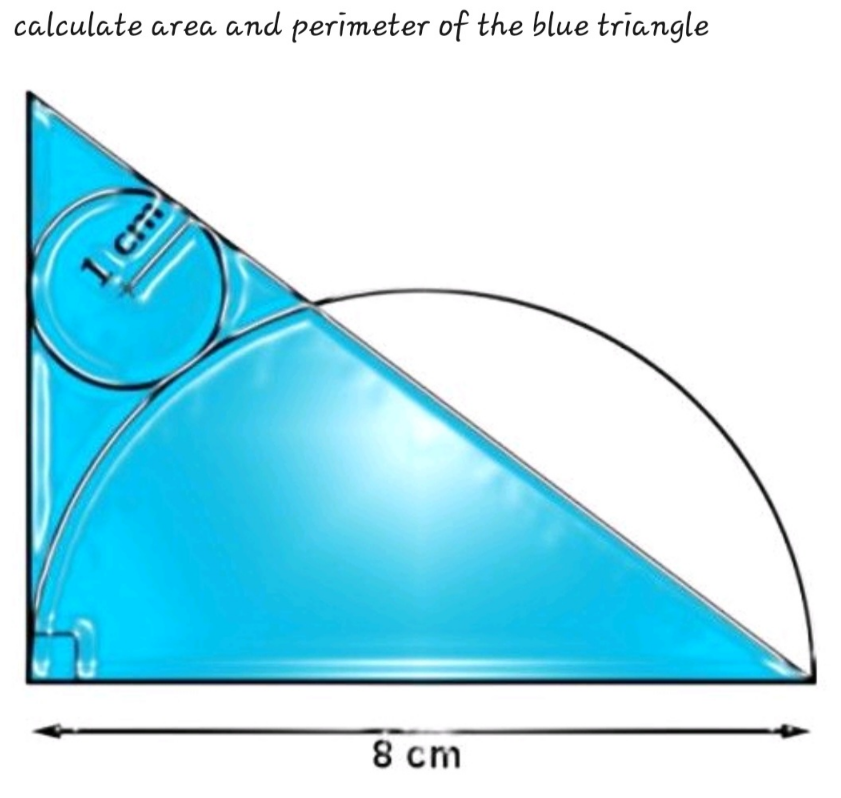
Answered by mr W last updated on 22/Apr/23

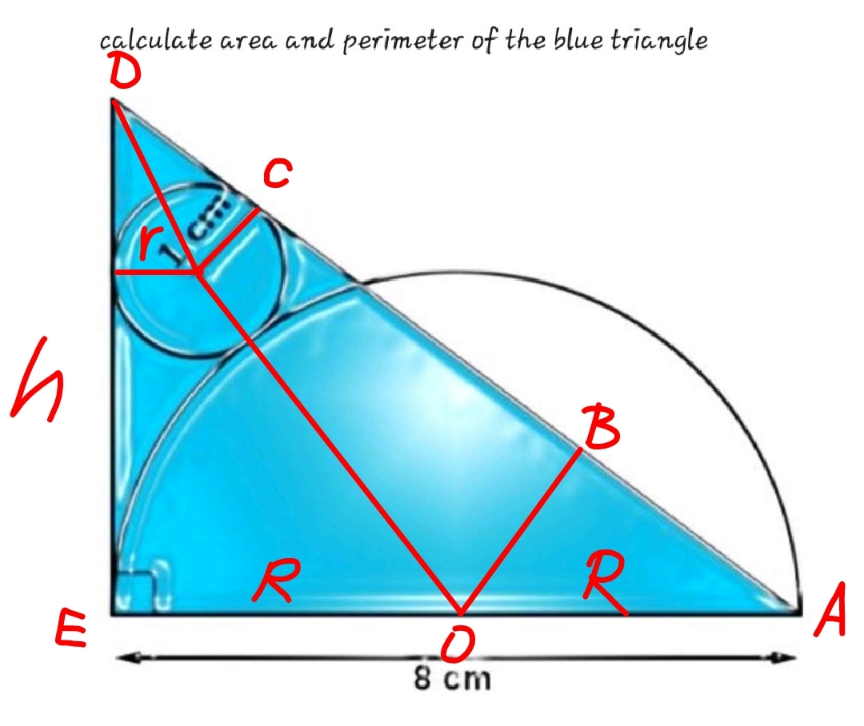
Commented by mr W last updated on 22/Apr/23

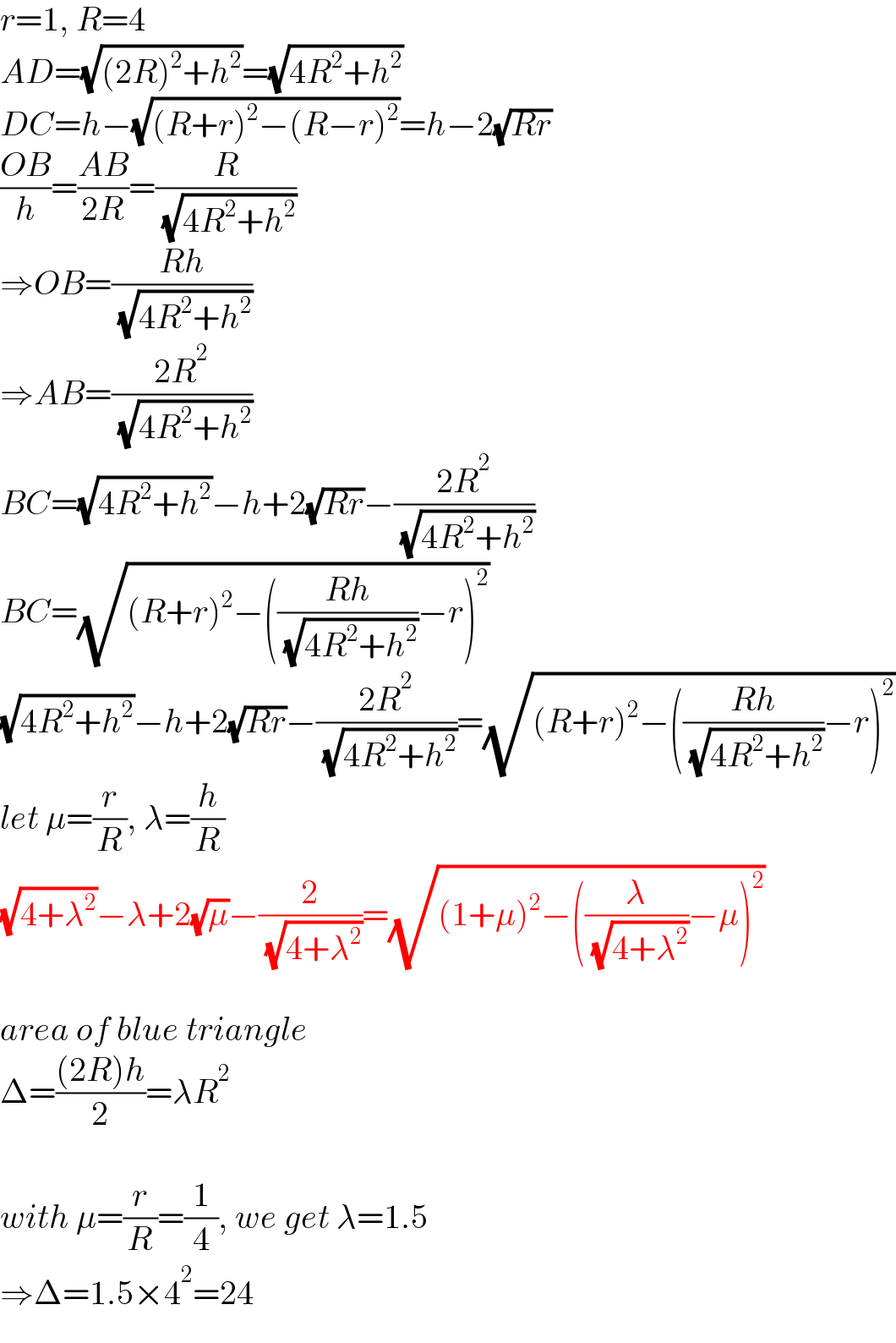
r=1, R=4 AD=(√((2R)^2 +h^2 ))=(√(4R^2 +h^2 )) DC=h−(√((R+r)^2 −(R−r)^2 ))=h−2(√(Rr)) ((OB)/h)=((AB)/(2R))=(R/( (√(4R^2 +h^2 )))) ⇒OB=((Rh)/( (√(4R^2 +h^2 )))) ⇒AB=((2R^2 )/( (√(4R^2 +h^2 )))) BC=(√(4R^2 +h^2 ))−h+2(√(Rr))−((2R^2 )/( (√(4R^2 +h^2 )))) BC=(√((R+r)^2 −(((Rh)/( (√(4R^2 +h^2 ))))−r)^2 )) (√(4R^2 +h^2 ))−h+2(√(Rr))−((2R^2 )/( (√(4R^2 +h^2 ))))=(√((R+r)^2 −(((Rh)/( (√(4R^2 +h^2 ))))−r)^2 )) let μ=(r/R), λ=(h/R) (√(4+λ^2 ))−λ+2(√μ)−(2/( (√(4+λ^2 ))))=(√((1+μ)^2 −((λ/( (√(4+λ^2 ))))−μ)^2 )) area of blue triangle Δ=(((2R)h)/2)=λR^2 with μ=(r/R)=(1/4), we get λ=1.5 ⇒Δ=1.5×4^2 =24

$${r}=\mathrm{1},\:{R}=\mathrm{4} \\ $$$${AD}=\sqrt{\left(\mathrm{2}{R}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} }=\sqrt{\mathrm{4}{R}^{\mathrm{2}} +{h}^{\mathrm{2}} } \\ $$$${DC}={h}−\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }={h}−\mathrm{2}\sqrt{{Rr}} \\ $$$$\frac{{OB}}{{h}}=\frac{{AB}}{\mathrm{2}{R}}=\frac{{R}}{\:\sqrt{\mathrm{4}{R}^{\mathrm{2}} +{h}^{\mathrm{2}} }} \\ $$$$\Rightarrow{OB}=\frac{{Rh}}{\:\sqrt{\mathrm{4}{R}^{\mathrm{2}} +{h}^{\mathrm{2}} }} \\ $$$$\Rightarrow{AB}=\frac{\mathrm{2}{R}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}{R}^{\mathrm{2}} +{h}^{\mathrm{2}} }} \\ $$$${BC}=\sqrt{\mathrm{4}{R}^{\mathrm{2}} +{h}^{\mathrm{2}} }−{h}+\mathrm{2}\sqrt{{Rr}}−\frac{\mathrm{2}{R}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}{R}^{\mathrm{2}} +{h}^{\mathrm{2}} }} \\ $$$${BC}=\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left(\frac{{Rh}}{\:\sqrt{\mathrm{4}{R}^{\mathrm{2}} +{h}^{\mathrm{2}} }}−{r}\right)^{\mathrm{2}} } \\ $$$$\sqrt{\mathrm{4}{R}^{\mathrm{2}} +{h}^{\mathrm{2}} }−{h}+\mathrm{2}\sqrt{{Rr}}−\frac{\mathrm{2}{R}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}{R}^{\mathrm{2}} +{h}^{\mathrm{2}} }}=\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left(\frac{{Rh}}{\:\sqrt{\mathrm{4}{R}^{\mathrm{2}} +{h}^{\mathrm{2}} }}−{r}\right)^{\mathrm{2}} } \\ $$$${let}\:\mu=\frac{{r}}{{R}},\:\lambda=\frac{{h}}{{R}} \\ $$$$\sqrt{\mathrm{4}+\lambda^{\mathrm{2}} }−\lambda+\mathrm{2}\sqrt{\mu}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}+\lambda^{\mathrm{2}} }}=\sqrt{\left(\mathrm{1}+\mu\right)^{\mathrm{2}} −\left(\frac{\lambda}{\:\sqrt{\mathrm{4}+\lambda^{\mathrm{2}} }}−\mu\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${area}\:{of}\:{blue}\:{triangle} \\ $$$$\Delta=\frac{\left(\mathrm{2}{R}\right){h}}{\mathrm{2}}=\lambda{R}^{\mathrm{2}} \\ $$$$ \\ $$$${with}\:\mu=\frac{{r}}{{R}}=\frac{\mathrm{1}}{\mathrm{4}},\:{we}\:{get}\:\lambda=\mathrm{1}.\mathrm{5} \\ $$$$\Rightarrow\Delta=\mathrm{1}.\mathrm{5}×\mathrm{4}^{\mathrm{2}} =\mathrm{24} \\ $$

Commented by Mingma last updated on 22/Apr/23

Excellent, sir!

Terms of Service

Privacy Policy

Contact: info@tinkutara.com