Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 191199 by 073 last updated on 20/Apr/23

Commented by 073 last updated on 20/Apr/23

sheed area=??

$$\mathrm{sheed}\:\mathrm{area}=?? \\ $$

Answered by cortano12 last updated on 20/Apr/23

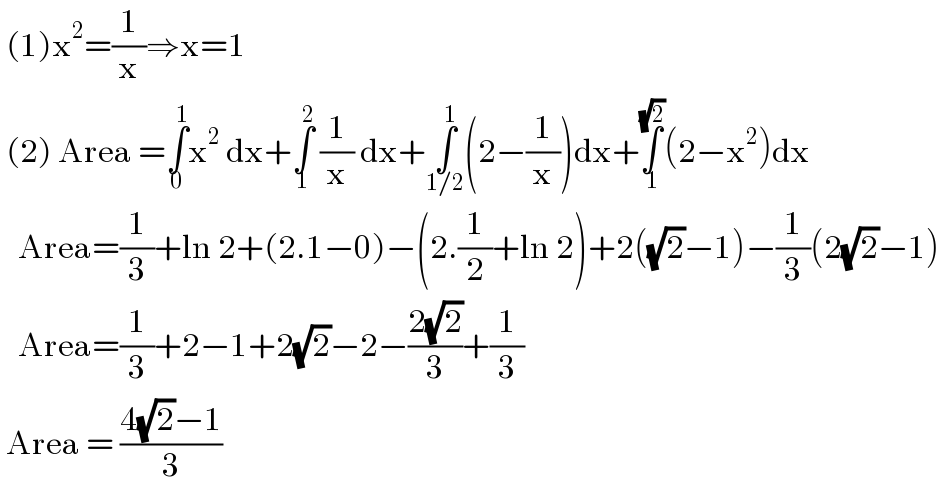
(1)x^2 =(1/x)⇒x=1 (2) Area =∫_0 ^1 x^2 dx+∫_1 ^2 (1/x) dx+∫_(1/2) ^1 (2−(1/x))dx+∫_1 ^(√2) (2−x^2 )dx Area=(1/3)+ln 2+(2.1−0)−(2.(1/2)+ln 2)+2((√2)−1)−(1/3)(2(√2)−1) Area=(1/3)+2−1+2(√2)−2−((2(√2))/3)+(1/3) Area = ((4(√2)−1)/3)

$$\:\left(\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{x}}\Rightarrow\mathrm{x}=\mathrm{1} \\ $$$$\:\left(\mathrm{2}\right)\:\mathrm{Area}\:=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{x}^{\mathrm{2}} \:\mathrm{dx}+\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{dx}+\underset{\mathrm{1}/\mathrm{2}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{dx}+\underset{\mathrm{1}} {\overset{\sqrt{\mathrm{2}}} {\int}}\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\:\:\:\mathrm{Area}=\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{ln}\:\mathrm{2}+\left(\mathrm{2}.\mathrm{1}−\mathrm{0}\right)−\left(\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{ln}\:\mathrm{2}\right)+\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\:\:\:\mathrm{Area}=\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{2}−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\mathrm{Area}\:=\:\frac{\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com