
Question Number 190624 by Rupesh123 last updated on 07/Apr/23
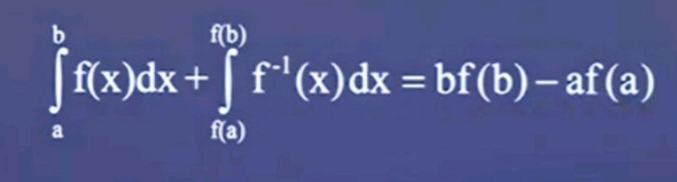
Answered by mr W last updated on 07/Apr/23
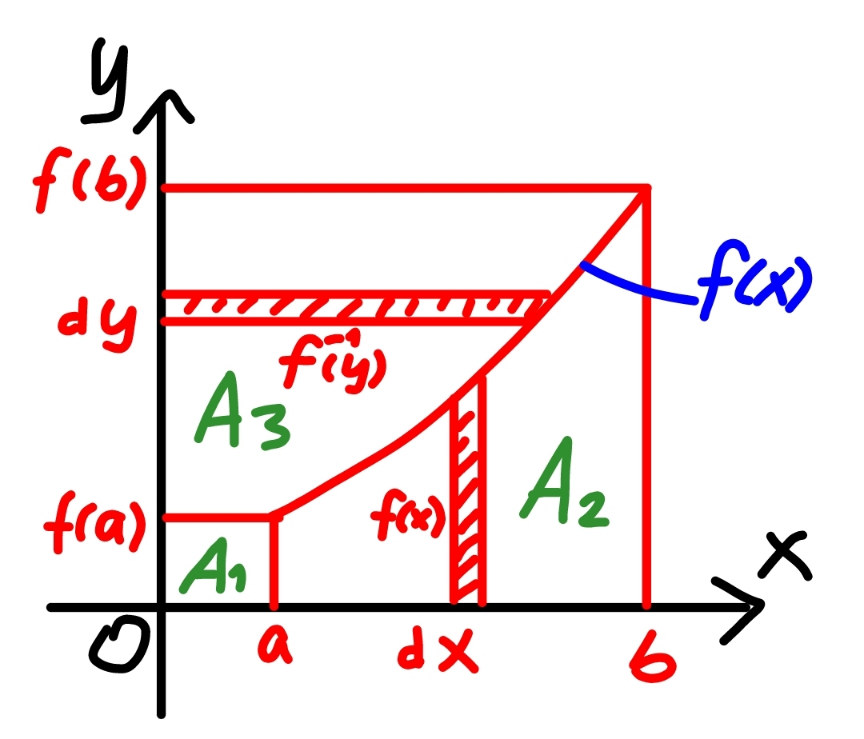
Commented by mr W last updated on 07/Apr/23
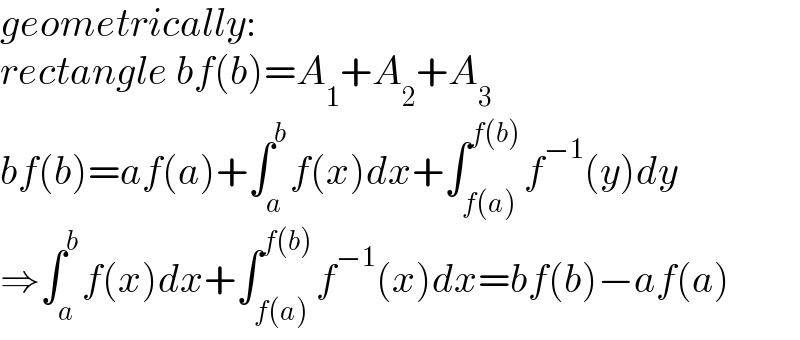
$${geometrically}: \\ $$$${rectangle}\:{bf}\left({b}\right)={A}_{\mathrm{1}} +{A}_{\mathrm{2}} +{A}_{\mathrm{3}} \\ $$$${bf}\left({b}\right)={af}\left({a}\right)+\int_{{a}} ^{{b}} {f}\left({x}\right){dx}+\int_{{f}\left({a}\right)} ^{{f}\left({b}\right)} {f}^{−\mathrm{1}} \left({y}\right){dy} \\ $$$$\Rightarrow\int_{{a}} ^{{b}} {f}\left({x}\right){dx}+\int_{{f}\left({a}\right)} ^{{f}\left({b}\right)} {f}^{−\mathrm{1}} \left({x}\right){dx}={bf}\left({b}\right)−{af}\left({a}\right) \\ $$
Commented by Rupesh123 last updated on 09/Apr/23
Excellent!
Answered by mehdee42 last updated on 08/Apr/23
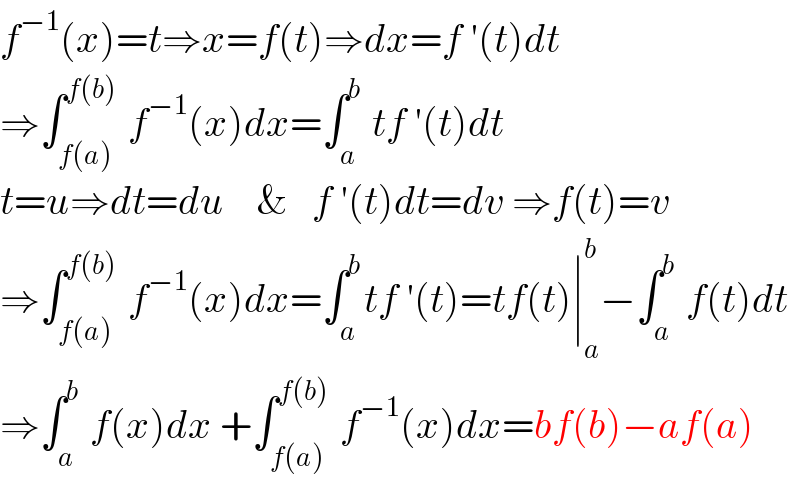
$${f}^{−\mathrm{1}} \left({x}\right)={t}\Rightarrow{x}={f}\left({t}\right)\Rightarrow{dx}={f}\:'\left({t}\right){dt} \\ $$$$\Rightarrow\int_{{f}\left({a}\right)} ^{{f}\left({b}\right)} \:{f}^{−\mathrm{1}} \left({x}\right){dx}=\int_{{a}} ^{{b}} \:{tf}\:'\left({t}\right){dt} \\ $$$${t}={u}\Rightarrow{dt}={du}\:\:\:\:\&\:\:\:{f}\:'\left({t}\right){dt}={dv}\:\Rightarrow{f}\left({t}\right)={v} \\ $$$$\Rightarrow\int_{{f}\left({a}\right)} ^{{f}\left({b}\right)} \:{f}^{−\mathrm{1}} \left({x}\right){dx}=\int_{{a}} ^{{b}} {tf}\:'\left({t}\right)={tf}\left({t}\right)\mid_{{a}} ^{{b}} −\int_{{a}} ^{{b}} \:{f}\left({t}\right){dt} \\ $$$$\Rightarrow\int_{{a}} ^{{b}} \:{f}\left({x}\right){dx}\:+\int_{{f}\left({a}\right)} ^{{f}\left({b}\right)} \:{f}^{−\mathrm{1}} \left({x}\right){dx}={bf}\left({b}\right)−{af}\left({a}\right) \\ $$
Commented by Rupesh123 last updated on 09/Apr/23
Excellent!
