Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 190527 by Rupesh123 last updated on 04/Apr/23

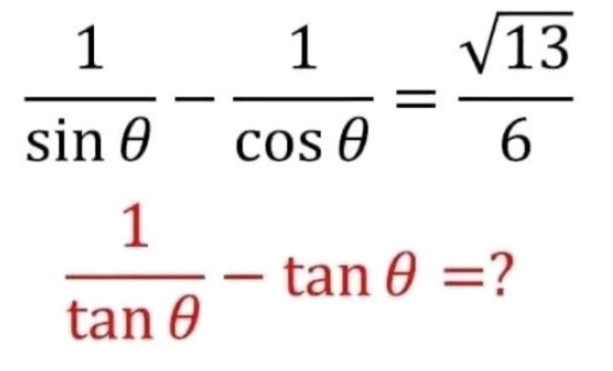
Commented by Frix last updated on 05/Apr/23

±(5/6)

$$\pm\frac{\mathrm{5}}{\mathrm{6}} \\ $$

Answered by cortano12 last updated on 05/Apr/23

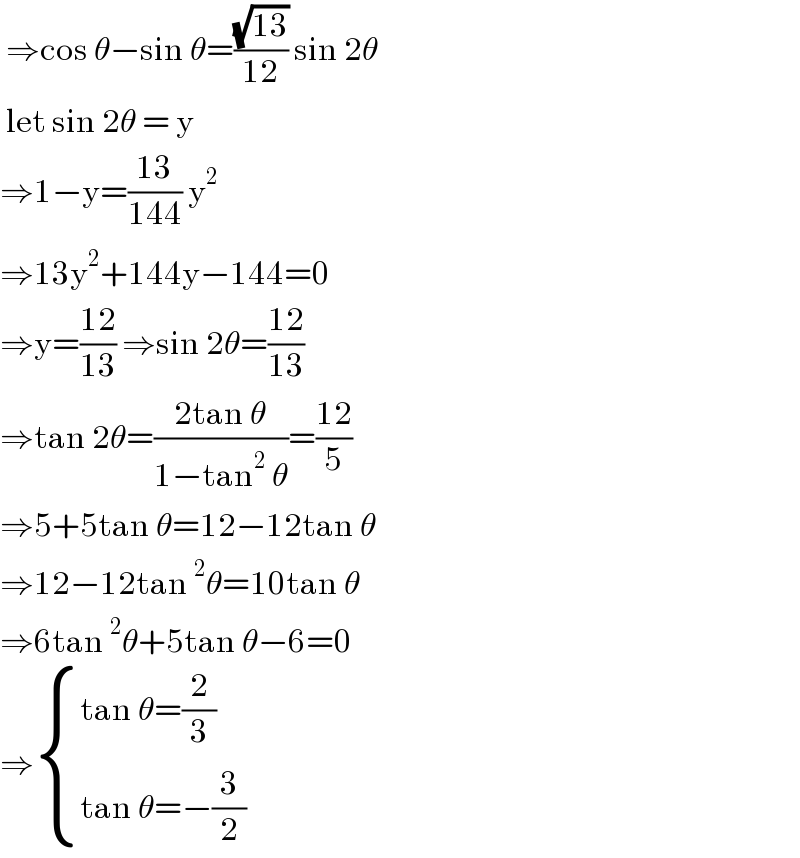
⇒cos θ−sin θ=((√(13))/(12)) sin 2θ let sin 2θ = y ⇒1−y=((13)/(144)) y^2 ⇒13y^2 +144y−144=0 ⇒y=((12)/(13)) ⇒sin 2θ=((12)/(13)) ⇒tan 2θ=((2tan θ)/(1−tan^2 θ))=((12)/5) ⇒5+5tan θ=12−12tan θ ⇒12−12tan^2 θ=10tan θ ⇒6tan^2 θ+5tan θ−6=0 ⇒ { ((tan θ=(2/3))),((tan θ=−(3/2))) :}

$$\:\Rightarrow\mathrm{cos}\:\theta−\mathrm{sin}\:\theta=\frac{\sqrt{\mathrm{13}}}{\mathrm{12}}\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\:\mathrm{let}\:\mathrm{sin}\:\mathrm{2}\theta\:=\:\mathrm{y} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{y}=\frac{\mathrm{13}}{\mathrm{144}}\:\mathrm{y}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{13y}^{\mathrm{2}} +\mathrm{144y}−\mathrm{144}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{12}}{\mathrm{13}}\:\Rightarrow\mathrm{sin}\:\mathrm{2}\theta=\frac{\mathrm{12}}{\mathrm{13}} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{2}\theta=\frac{\mathrm{2tan}\:\theta}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\theta}=\frac{\mathrm{12}}{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{5}+\mathrm{5tan}\:\theta=\mathrm{12}−\mathrm{12tan}\:\theta \\ $$$$\Rightarrow\mathrm{12}−\mathrm{12tan}\:^{\mathrm{2}} \theta=\mathrm{10tan}\:\theta \\ $$$$\Rightarrow\mathrm{6tan}\:^{\mathrm{2}} \theta+\mathrm{5tan}\:\theta−\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{\mathrm{tan}\:\theta=\frac{\mathrm{2}}{\mathrm{3}}}\\{\mathrm{tan}\:\theta=−\frac{\mathrm{3}}{\mathrm{2}}}\end{cases} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com