
Question Number 190169 by sonukgindia last updated on 29/Mar/23
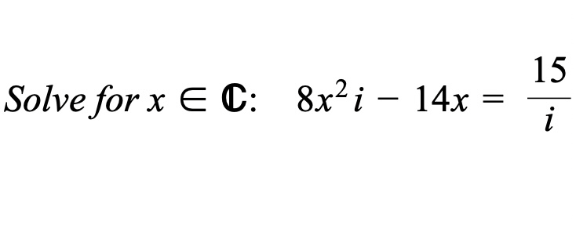
Commented by Frix last updated on 29/Mar/23

$$\mathrm{Folks}\:\mathrm{2}\:\mathrm{questions}: \\ $$$$\left(\mathrm{1}\right)\:\mathrm{How}\:\mathrm{many}\:\mathrm{solutions}\:\mathrm{does}\:\mathrm{a}\:\mathrm{polynome} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{of}\:\mathrm{degree}\:{n}\:\mathrm{have}? \\ $$$$\left(\mathrm{2}\right)\:\mathrm{Do}\:\mathrm{you}\:\mathrm{ever}\:\mathrm{test}\:\mathrm{your}\:\mathrm{solutions}? \\ $$
Commented by Frix last updated on 29/Mar/23
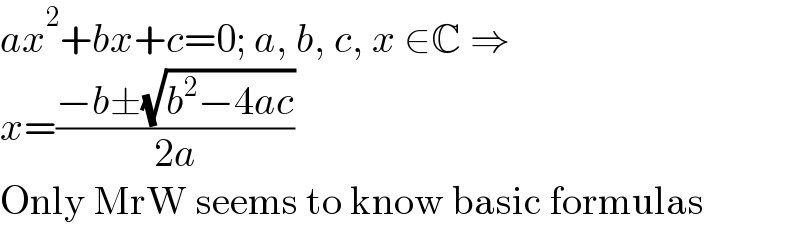
$${ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0};\:{a},\:{b},\:{c},\:{x}\:\in\mathbb{C}\:\Rightarrow \\ $$$${x}=\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}} \\ $$$$\mathrm{Only}\:\mathrm{MrW}\:\mathrm{seems}\:\mathrm{to}\:\mathrm{know}\:\mathrm{basic}\:\mathrm{formulas} \\ $$
Commented by Frix last updated on 29/Mar/23
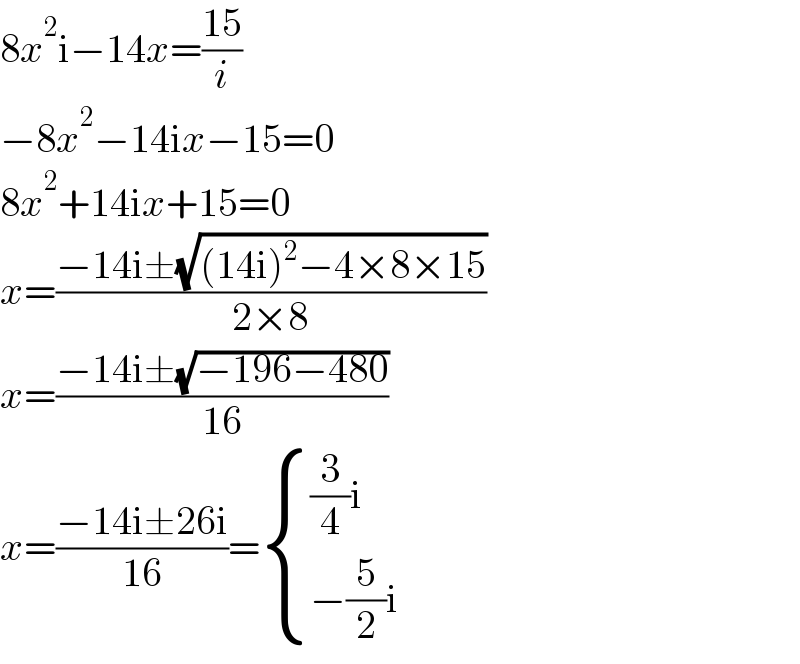
$$\mathrm{8}{x}^{\mathrm{2}} \mathrm{i}−\mathrm{14}{x}=\frac{\mathrm{15}}{{i}} \\ $$$$−\mathrm{8}{x}^{\mathrm{2}} −\mathrm{14i}{x}−\mathrm{15}=\mathrm{0} \\ $$$$\mathrm{8}{x}^{\mathrm{2}} +\mathrm{14i}{x}+\mathrm{15}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{14i}\pm\sqrt{\left(\mathrm{14i}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{8}×\mathrm{15}}}{\mathrm{2}×\mathrm{8}} \\ $$$${x}=\frac{−\mathrm{14i}\pm\sqrt{−\mathrm{196}−\mathrm{480}}}{\mathrm{16}} \\ $$$${x}=\frac{−\mathrm{14i}\pm\mathrm{26i}}{\mathrm{16}}=\begin{cases}{\frac{\mathrm{3}}{\mathrm{4}}\mathrm{i}}\\{−\frac{\mathrm{5}}{\mathrm{2}}\mathrm{i}}\end{cases} \\ $$
Answered by Rasheed.Sindhi last updated on 29/Mar/23
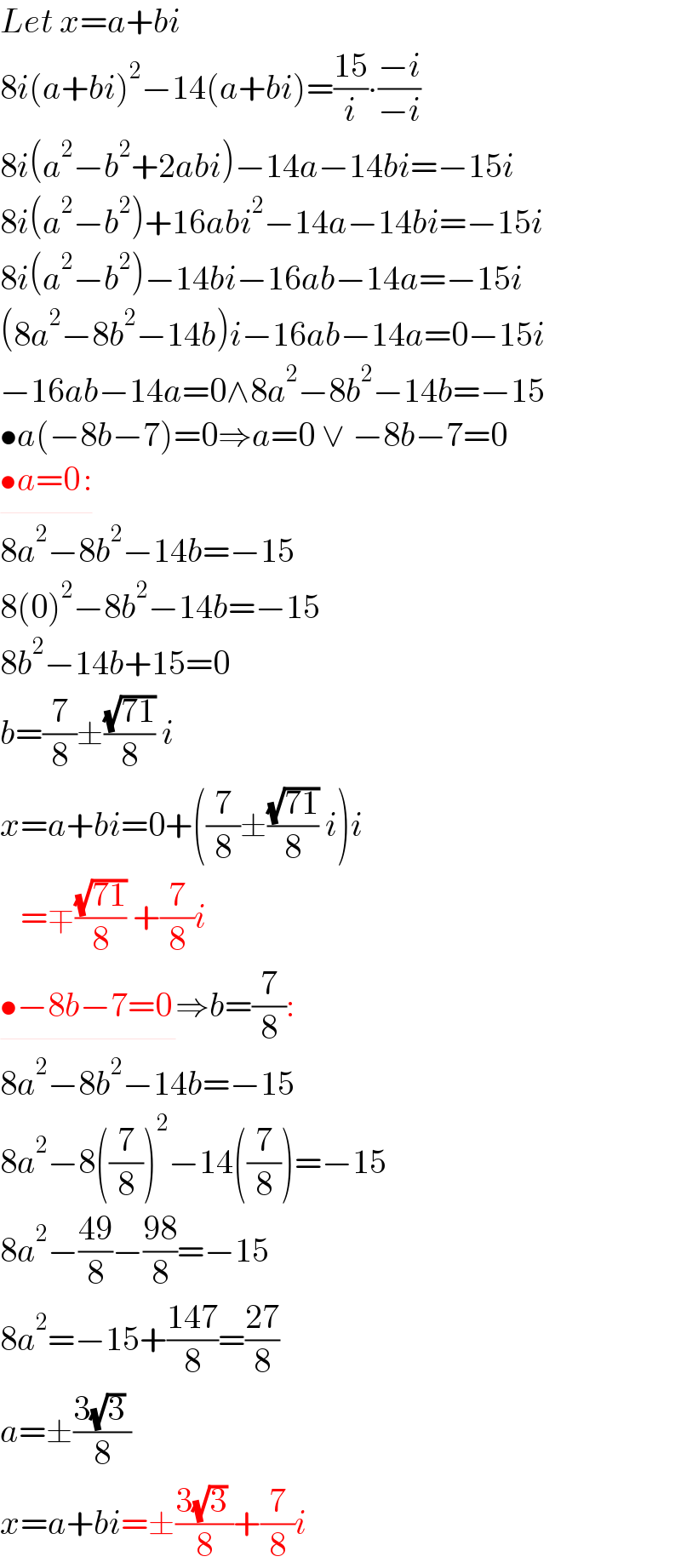
$${Let}\:{x}={a}+{bi} \\ $$$$\mathrm{8}{i}\left({a}+{bi}\right)^{\mathrm{2}} −\mathrm{14}\left({a}+{bi}\right)=\frac{\mathrm{15}}{{i}}\centerdot\frac{−{i}}{−{i}} \\ $$$$\mathrm{8}{i}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{2}{abi}\right)−\mathrm{14}{a}−\mathrm{14}{bi}=−\mathrm{15}{i} \\ $$$$\mathrm{8}{i}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+\mathrm{16}{abi}^{\mathrm{2}} −\mathrm{14}{a}−\mathrm{14}{bi}=−\mathrm{15}{i} \\ $$$$\mathrm{8}{i}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)−\mathrm{14}{bi}−\mathrm{16}{ab}−\mathrm{14}{a}=−\mathrm{15}{i} \\ $$$$\left(\mathrm{8}{a}^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}\right){i}−\mathrm{16}{ab}−\mathrm{14}{a}=\mathrm{0}−\mathrm{15}{i} \\ $$$$−\mathrm{16}{ab}−\mathrm{14}{a}=\mathrm{0}\wedge\mathrm{8}{a}^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}=−\mathrm{15} \\ $$$$\bullet{a}\left(−\mathrm{8}{b}−\mathrm{7}\right)=\mathrm{0}\Rightarrow{a}=\mathrm{0}\:\vee\:−\mathrm{8}{b}−\mathrm{7}=\mathrm{0} \\ $$$$\underline{\bullet{a}=\mathrm{0}_{\:} :} \\ $$$$\mathrm{8}{a}^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}=−\mathrm{15} \\ $$$$\mathrm{8}\left(\mathrm{0}\right)^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}=−\mathrm{15} \\ $$$$\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}+\mathrm{15}=\mathrm{0} \\ $$$${b}=\frac{\mathrm{7}}{\mathrm{8}}\pm\frac{\sqrt{\mathrm{71}}}{\mathrm{8}}\:{i} \\ $$$${x}={a}+{bi}=\mathrm{0}+\left(\frac{\mathrm{7}}{\mathrm{8}}\pm\frac{\sqrt{\mathrm{71}}}{\mathrm{8}}\:{i}\right){i} \\ $$$$\:\:\:=\mp\frac{\sqrt{\mathrm{71}}}{\mathrm{8}}\:+\frac{\mathrm{7}}{\mathrm{8}}{i} \\ $$$$\underline{\bullet−\mathrm{8}{b}−\mathrm{7}=\mathrm{0}_{\:} }\Rightarrow{b}=\frac{\mathrm{7}}{\mathrm{8}}: \\ $$$$\mathrm{8}{a}^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}=−\mathrm{15} \\ $$$$\mathrm{8}{a}^{\mathrm{2}} −\mathrm{8}\left(\frac{\mathrm{7}}{\mathrm{8}}\right)^{\mathrm{2}} −\mathrm{14}\left(\frac{\mathrm{7}}{\mathrm{8}}\right)=−\mathrm{15} \\ $$$$\mathrm{8}{a}^{\mathrm{2}} −\frac{\mathrm{49}}{\mathrm{8}}−\frac{\mathrm{98}}{\mathrm{8}}=−\mathrm{15} \\ $$$$\mathrm{8}{a}^{\mathrm{2}} =−\mathrm{15}+\frac{\mathrm{147}}{\mathrm{8}}=\frac{\mathrm{27}}{\mathrm{8}} \\ $$$${a}=\pm\frac{\mathrm{3}\sqrt{\mathrm{3}}\:}{\mathrm{8}} \\ $$$${x}={a}+{bi}=\pm\frac{\mathrm{3}\sqrt{\mathrm{3}}\:}{\mathrm{8}}+\frac{\mathrm{7}}{\mathrm{8}}{i} \\ $$
Commented by JDamian last updated on 29/Mar/23
there is a -14b that it should be +14b
Commented by mehdee42 last updated on 29/Mar/23
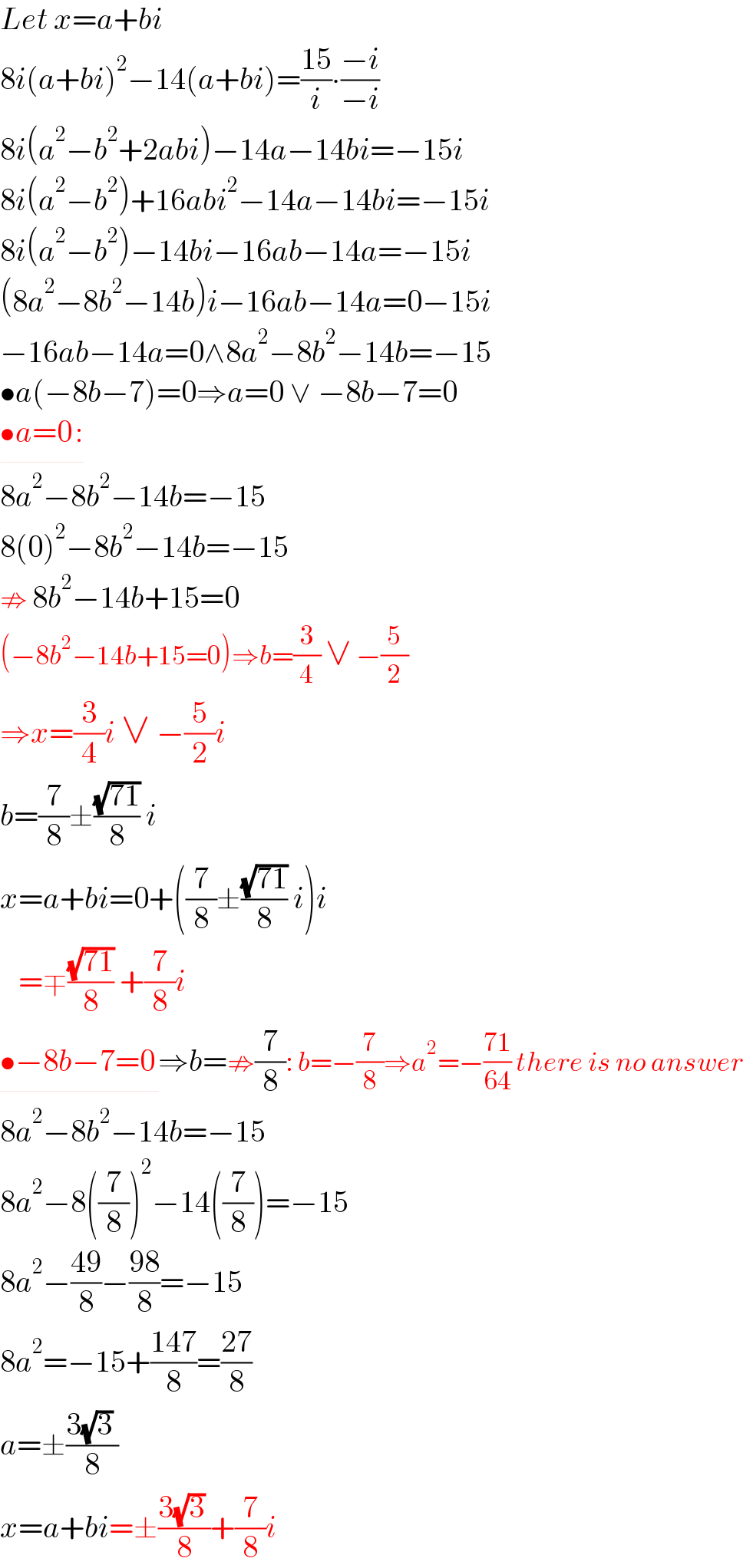
$${Let}\:{x}={a}+{bi} \\ $$$$\mathrm{8}{i}\left({a}+{bi}\right)^{\mathrm{2}} −\mathrm{14}\left({a}+{bi}\right)=\frac{\mathrm{15}}{{i}}\centerdot\frac{−{i}}{−{i}} \\ $$$$\mathrm{8}{i}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{2}{abi}\right)−\mathrm{14}{a}−\mathrm{14}{bi}=−\mathrm{15}{i} \\ $$$$\mathrm{8}{i}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+\mathrm{16}{abi}^{\mathrm{2}} −\mathrm{14}{a}−\mathrm{14}{bi}=−\mathrm{15}{i} \\ $$$$\mathrm{8}{i}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)−\mathrm{14}{bi}−\mathrm{16}{ab}−\mathrm{14}{a}=−\mathrm{15}{i} \\ $$$$\left(\mathrm{8}{a}^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}\right){i}−\mathrm{16}{ab}−\mathrm{14}{a}=\mathrm{0}−\mathrm{15}{i} \\ $$$$−\mathrm{16}{ab}−\mathrm{14}{a}=\mathrm{0}\wedge\mathrm{8}{a}^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}=−\mathrm{15} \\ $$$$\bullet{a}\left(−\mathrm{8}{b}−\mathrm{7}\right)=\mathrm{0}\Rightarrow{a}=\mathrm{0}\:\vee\:−\mathrm{8}{b}−\mathrm{7}=\mathrm{0} \\ $$$$\underline{\bullet{a}=\mathrm{0}_{\:} :} \\ $$$$\mathrm{8}{a}^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}=−\mathrm{15} \\ $$$$\mathrm{8}\left(\mathrm{0}\right)^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}=−\mathrm{15} \\ $$$$\nRightarrow\:\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}+\mathrm{15}=\mathrm{0}\:\: \\ $$$$\left(−\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}+\mathrm{15}=\mathrm{0}\right)\Rightarrow{b}=\frac{\mathrm{3}}{\mathrm{4}}\:\vee\:−\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}}{\mathrm{4}}{i}\:\vee\:−\frac{\mathrm{5}}{\mathrm{2}}{i} \\ $$$${b}=\frac{\mathrm{7}}{\mathrm{8}}\pm\frac{\sqrt{\mathrm{71}}}{\mathrm{8}}\:{i} \\ $$$${x}={a}+{bi}=\mathrm{0}+\left(\frac{\mathrm{7}}{\mathrm{8}}\pm\frac{\sqrt{\mathrm{71}}}{\mathrm{8}}\:{i}\right){i} \\ $$$$\:\:\:=\mp\frac{\sqrt{\mathrm{71}}}{\mathrm{8}}\:+\frac{\mathrm{7}}{\mathrm{8}}{i} \\ $$$$\underline{\bullet−\mathrm{8}{b}−\mathrm{7}=\mathrm{0}_{\:} }\Rightarrow{b}=\nRightarrow\frac{\mathrm{7}}{\mathrm{8}}:\:{b}=−\frac{\mathrm{7}}{\mathrm{8}}\Rightarrow{a}^{\mathrm{2}} =−\frac{\mathrm{71}}{\mathrm{64}}\:{there}\:{is}\:{no}\:{answer} \\ $$$$\mathrm{8}{a}^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}=−\mathrm{15} \\ $$$$\mathrm{8}{a}^{\mathrm{2}} −\mathrm{8}\left(\frac{\mathrm{7}}{\mathrm{8}}\right)^{\mathrm{2}} −\mathrm{14}\left(\frac{\mathrm{7}}{\mathrm{8}}\right)=−\mathrm{15} \\ $$$$\mathrm{8}{a}^{\mathrm{2}} −\frac{\mathrm{49}}{\mathrm{8}}−\frac{\mathrm{98}}{\mathrm{8}}=−\mathrm{15} \\ $$$$\mathrm{8}{a}^{\mathrm{2}} =−\mathrm{15}+\frac{\mathrm{147}}{\mathrm{8}}=\frac{\mathrm{27}}{\mathrm{8}} \\ $$$${a}=\pm\frac{\mathrm{3}\sqrt{\mathrm{3}}\:}{\mathrm{8}} \\ $$$${x}={a}+{bi}=\pm\frac{\mathrm{3}\sqrt{\mathrm{3}}\:}{\mathrm{8}}+\frac{\mathrm{7}}{\mathrm{8}}{i} \\ $$
Commented by Frix last updated on 29/Mar/23

$$\mathrm{So}\:\mathrm{you}\:\mathrm{get}\:\mathrm{4}\:\mathrm{solutions}?! \\ $$$$\mathrm{You}\:\mathrm{seriously}\:\mathrm{claim}\:\mathrm{that}: \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}= \\ $$$$={a}\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)\left({x}−{x}_{\mathrm{3}} \right)\left({x}−{x}_{\mathrm{4}} \right) \\ $$$$\Leftrightarrow \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}= \\ $$$$={a}\left({x}^{\mathrm{4}} +{Ax}^{\mathrm{3}} +{Bx}^{\mathrm{2}} +{Cx}+{D}\right) \\ $$$$\mathrm{A}\:\mathrm{miracle}! \\ $$
Commented by Rasheed.Sindhi last updated on 29/Mar/23

$$\left.{No}\:{miracle}\:{sir}\::\right) \\ $$$${Some}\:{solutions}\:{are}\:{invalid}.\:{I}\:{should} \\ $$$${have}\:{tested}.{Anyway}\:{my}\:{mistake}\:{sir}! \\ $$
Commented by Rasheed.Sindhi last updated on 29/Mar/23
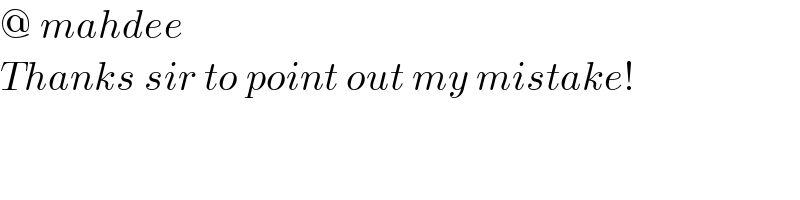
$$@\:{mahdee} \\ $$$${Thanks}\:{sir}\:{to}\:{point}\:{out}\:{my}\:{mistake}! \\ $$
Commented by MJS_new last updated on 29/Mar/23
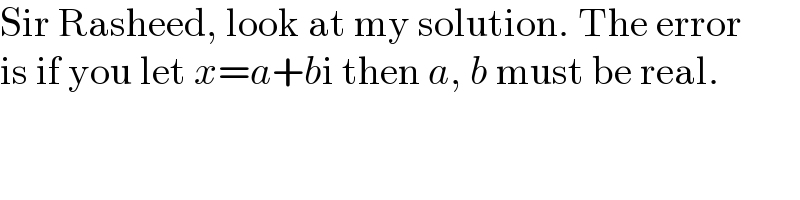
$$\mathrm{Sir}\:\mathrm{Rasheed},\:\mathrm{look}\:\mathrm{at}\:\mathrm{my}\:\mathrm{solution}.\:\mathrm{The}\:\mathrm{error} \\ $$$$\mathrm{is}\:\mathrm{if}\:\mathrm{you}\:\mathrm{let}\:{x}={a}+{b}\mathrm{i}\:\mathrm{then}\:{a},\:{b}\:\mathrm{must}\:\mathrm{be}\:\mathrm{real}. \\ $$
Commented by Rasheed.Sindhi last updated on 29/Mar/23
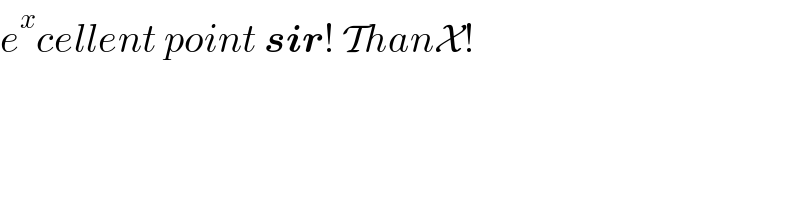
$${e}^{{x}} {cellent}\:{point}\:\boldsymbol{{sir}}!\:\mathcal{T}{han}\mathcal{X}! \\ $$
Commented by mehdee42 last updated on 29/Mar/23

$${I}\:{Thank}\:{you}\:{too}.{your}\:{solution}\:{is}\:{certainly}\: \\ $$$${very}\:{beautiful}. \\ $$
Commented by Rasheed.Sindhi last updated on 30/Mar/23
��
Answered by mr W last updated on 29/Mar/23
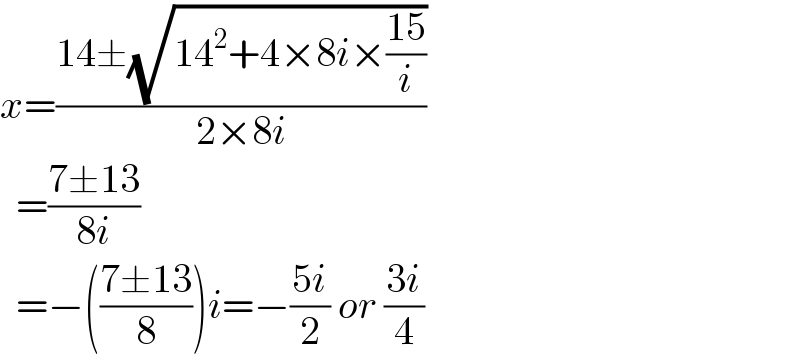
$${x}=\frac{\mathrm{14}\pm\sqrt{\mathrm{14}^{\mathrm{2}} +\mathrm{4}×\mathrm{8}{i}×\frac{\mathrm{15}}{{i}}}}{\mathrm{2}×\mathrm{8}{i}} \\ $$$$\:\:=\frac{\mathrm{7}\pm\mathrm{13}}{\mathrm{8}{i}} \\ $$$$\:\:=−\left(\frac{\mathrm{7}\pm\mathrm{13}}{\mathrm{8}}\right){i}=−\frac{\mathrm{5}{i}}{\mathrm{2}}\:{or}\:\frac{\mathrm{3}{i}}{\mathrm{4}} \\ $$
Commented by Rasheed.Sindhi last updated on 31/Mar/23

$$\mathbb{N}\boldsymbol{\mathrm{i}}\subset\in\:\boldsymbol{\mathrm{Sir}}! \\ $$
Answered by MJS_new last updated on 29/Mar/23
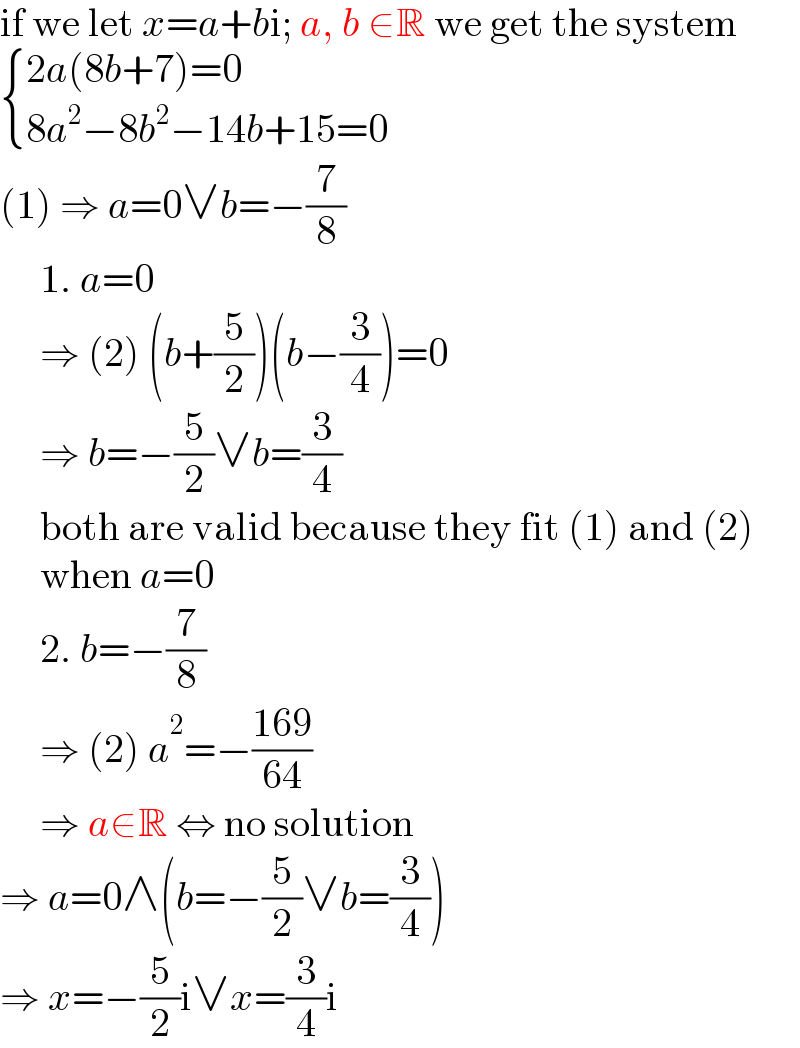
$$\mathrm{if}\:\mathrm{we}\:\mathrm{let}\:{x}={a}+{b}\mathrm{i};\:{a},\:{b}\:\in\mathbb{R}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{system} \\ $$$$\begin{cases}{\mathrm{2}{a}\left(\mathrm{8}{b}+\mathrm{7}\right)=\mathrm{0}}\\{\mathrm{8}{a}^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} −\mathrm{14}{b}+\mathrm{15}=\mathrm{0}}\end{cases} \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow\:{a}=\mathrm{0}\vee{b}=−\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$\:\:\:\:\:\mathrm{1}.\:{a}=\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\:\left(\mathrm{2}\right)\:\left({b}+\frac{\mathrm{5}}{\mathrm{2}}\right)\left({b}−\frac{\mathrm{3}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\:{b}=−\frac{\mathrm{5}}{\mathrm{2}}\vee{b}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\mathrm{both}\:\mathrm{are}\:\mathrm{valid}\:\mathrm{because}\:\mathrm{they}\:\mathrm{fit}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\mathrm{when}\:{a}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{2}.\:{b}=−\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$\:\:\:\:\:\Rightarrow\:\left(\mathrm{2}\right)\:{a}^{\mathrm{2}} =−\frac{\mathrm{169}}{\mathrm{64}} \\ $$$$\:\:\:\:\:\Rightarrow\:{a}\notin\mathbb{R}\:\Leftrightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\Rightarrow\:{a}=\mathrm{0}\wedge\left({b}=−\frac{\mathrm{5}}{\mathrm{2}}\vee{b}=\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$\Rightarrow\:{x}=−\frac{\mathrm{5}}{\mathrm{2}}\mathrm{i}\vee{x}=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{i} \\ $$
Commented by Rasheed.Sindhi last updated on 29/Mar/23

$$\cap\boldsymbol{\mathrm{i}}\subset\in! \\ $$$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{sir}}! \\ $$
