Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 190094 by mnjuly1970 last updated on 27/Mar/23

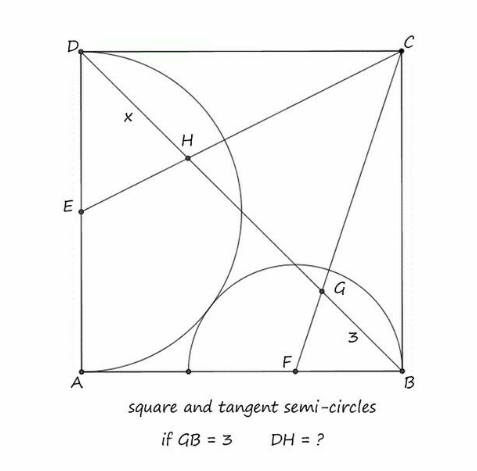
Answered by a.lgnaoui last updated on 28/Mar/23

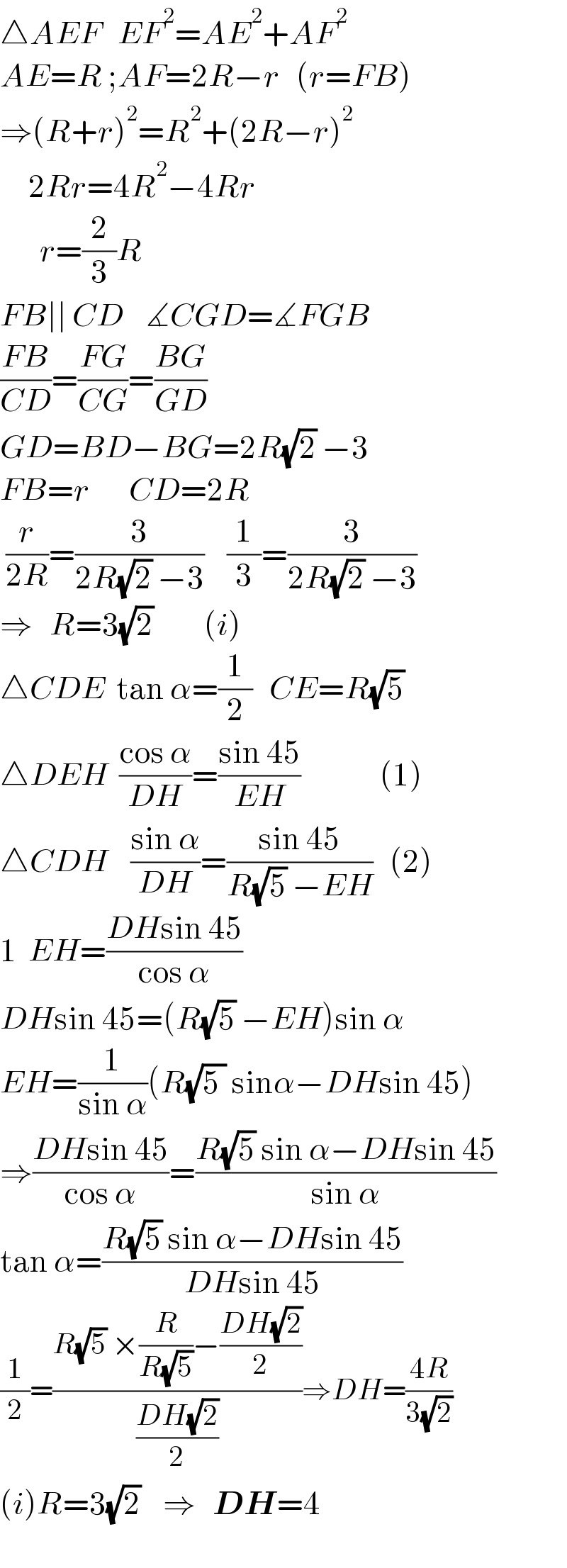
△AEF EF^2 =AE^2 +AF^2 AE=R ;AF=2R−r (r=FB) ⇒(R+r)^2 =R^2 +(2R−r)^2 2Rr=4R^2 −4Rr r=(2/3)R FB∣∣ CD ∡CGD=∡FGB ((FB)/(CD))=((FG)/(CG))=((BG)/(GD)) GD=BD−BG=2R(√2) −3 FB=r CD=2R (r/(2R))=(3/(2R(√2) −3)) (1/3)=(3/(2R(√2) −3)) ⇒ R=3(√2) (i) △CDE tan α=(1/2) CE=R(√5) △DEH ((cos α)/(DH))=((sin 45)/(EH)) (1) △CDH ((sin α)/(DH))=((sin 45)/(R(√5) −EH)) (2) 1 EH=((DHsin 45)/(cos α)) DHsin 45=(R(√5) −EH)sin α EH=(1/(sin α))(R(√(5 )) sinα−DHsin 45) ⇒((DHsin 45)/(cos α))=((R(√5) sin α−DHsin 45)/(sin α)) tan α=((R(√5) sin α−DHsin 45)/(DHsin 45)) (1/2)=((R(√5) ×(R/(R(√5)))−((DH(√2))/2))/((DH(√2))/2))⇒DH=((4R)/(3(√2))) (i)R=3(√2) ⇒ DH=4

$$\bigtriangleup{AEF}\:\:\:{EF}^{\mathrm{2}} ={AE}^{\mathrm{2}} +{AF}^{\mathrm{2}} \\ $$$${AE}={R}\:;{AF}=\mathrm{2}{R}−{r}\:\:\:\left({r}={FB}\right) \\ $$$$\Rightarrow\left({R}+{r}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} +\left(\mathrm{2}{R}−{r}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{2}{Rr}=\mathrm{4}{R}^{\mathrm{2}} −\mathrm{4}{Rr}\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:{r}=\frac{\mathrm{2}}{\mathrm{3}}{R} \\ $$$${FB}\mid\mid\:{CD}\:\:\:\:\measuredangle{CGD}=\measuredangle{FGB} \\ $$$$\frac{{FB}}{{CD}}=\frac{{FG}}{{CG}}=\frac{{BG}}{{GD}}\:\: \\ $$$${GD}={BD}−{BG}=\mathrm{2}{R}\sqrt{\mathrm{2}}\:−\mathrm{3} \\ $$$${FB}={r}\:\:\:\:\:\:\:{CD}=\mathrm{2}{R} \\ $$$$\:\frac{{r}}{\mathrm{2}{R}}=\frac{\mathrm{3}}{\mathrm{2}{R}\sqrt{\mathrm{2}}\:−\mathrm{3}}\:\:\:\:\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{3}}{\mathrm{2}{R}\sqrt{\mathrm{2}}\:−\mathrm{3}} \\ $$$$\Rightarrow\:\:\:{R}=\mathrm{3}\sqrt{\mathrm{2}}\:\:\:\:\:\:\:\:\:\left({i}\right) \\ $$$$\bigtriangleup{CDE}\:\:\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:{CE}={R}\sqrt{\mathrm{5}} \\ $$$$\bigtriangleup{DEH}\:\:\frac{\mathrm{cos}\:\alpha}{{DH}}=\frac{\mathrm{sin}\:\mathrm{45}}{{EH}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\bigtriangleup{CDH}\:\:\:\:\frac{\mathrm{sin}\:\alpha}{{DH}}=\frac{\mathrm{sin}\:\mathrm{45}}{{R}\sqrt{\mathrm{5}}\:−{EH}}\:\:\:\left(\mathrm{2}\right) \\ $$$$\mathrm{1}\:\:{EH}=\frac{{DH}\mathrm{sin}\:\mathrm{45}}{\mathrm{cos}\:\alpha} \\ $$$${DH}\mathrm{sin}\:\mathrm{45}=\left({R}\sqrt{\mathrm{5}}\:−{EH}\right)\mathrm{sin}\:\alpha \\ $$$${EH}=\frac{\mathrm{1}}{\mathrm{sin}\:\alpha}\left({R}\sqrt{\mathrm{5}\:}\:\mathrm{sin}\alpha−{DH}\mathrm{sin}\:\mathrm{45}\right) \\ $$$$\Rightarrow\frac{{DH}\mathrm{sin}\:\mathrm{45}}{\mathrm{cos}\:\alpha}=\frac{{R}\sqrt{\mathrm{5}}\:\mathrm{sin}\:\alpha−{DH}\mathrm{sin}\:\mathrm{45}}{\mathrm{sin}\:\alpha} \\ $$$$\mathrm{tan}\:\alpha=\frac{{R}\sqrt{\mathrm{5}}\:\mathrm{sin}\:\alpha−{DH}\mathrm{sin}\:\mathrm{45}}{{DH}\mathrm{sin}\:\mathrm{45}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}=\frac{{R}\sqrt{\mathrm{5}}\:×\frac{{R}}{{R}\sqrt{\mathrm{5}}}−\frac{{DH}\sqrt{\mathrm{2}}}{\mathrm{2}}}{\frac{{DH}\sqrt{\mathrm{2}}}{\mathrm{2}}}\Rightarrow{DH}=\frac{\mathrm{4}{R}}{\mathrm{3}\sqrt{\mathrm{2}}} \\ $$$$\left({i}\right){R}=\mathrm{3}\sqrt{\mathrm{2}}\:\:\:\:\Rightarrow\:\:\:\boldsymbol{{DH}}=\mathrm{4}\:\: \\ $$$$ \\ $$

Commented by a.lgnaoui last updated on 28/Mar/23

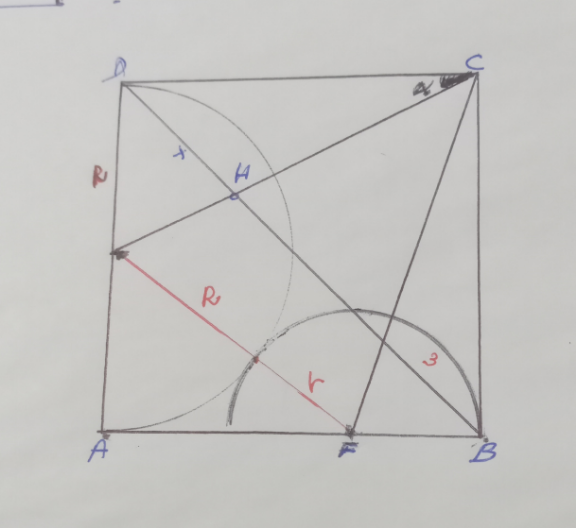
Answered by mr W last updated on 29/Mar/23

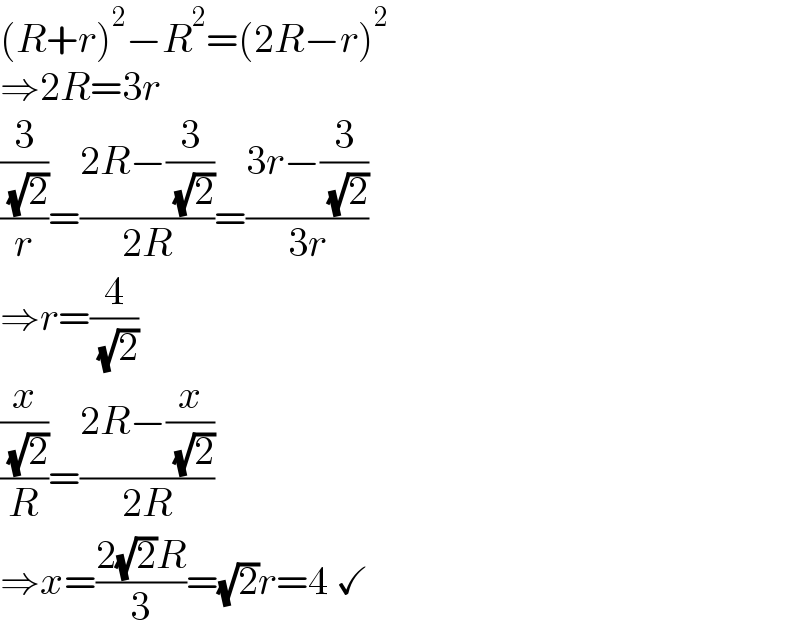
(R+r)^2 −R^2 =(2R−r)^2 ⇒2R=3r ((3/( (√2)))/r)=((2R−(3/( (√2))))/(2R))=((3r−(3/( (√2))))/(3r)) ⇒r=(4/( (√2))) ((x/( (√2)))/R)=((2R−(x/( (√2))))/(2R)) ⇒x=((2(√2)R)/3)=(√2)r=4 ✓

$$\left({R}+{r}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} =\left(\mathrm{2}{R}−{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{R}=\mathrm{3}{r} \\ $$$$\frac{\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}}{{r}}=\frac{\mathrm{2}{R}−\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}}{\mathrm{2}{R}}=\frac{\mathrm{3}{r}−\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}}{\mathrm{3}{r}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}}} \\ $$$$\frac{\frac{{x}}{\:\sqrt{\mathrm{2}}}}{{R}}=\frac{\mathrm{2}{R}−\frac{{x}}{\:\sqrt{\mathrm{2}}}}{\mathrm{2}{R}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}\sqrt{\mathrm{2}}{R}}{\mathrm{3}}=\sqrt{\mathrm{2}}{r}=\mathrm{4}\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com