
Question Number 190009 by Rupesh123 last updated on 26/Mar/23

Commented by Frix last updated on 26/Mar/23
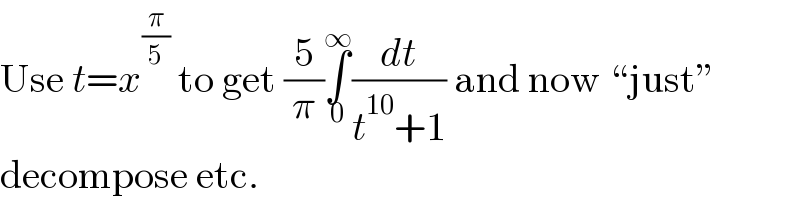
$$\mathrm{Use}\:{t}={x}^{\frac{\pi}{\mathrm{5}}} \:\mathrm{to}\:\mathrm{get}\:\frac{\mathrm{5}}{\pi}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{10}} +\mathrm{1}}\:\mathrm{and}\:\mathrm{now}\:``\mathrm{just}'' \\ $$$$\mathrm{decompose}\:\mathrm{etc}. \\ $$
Commented by ARUNG_Brandon_MBU last updated on 27/Mar/23
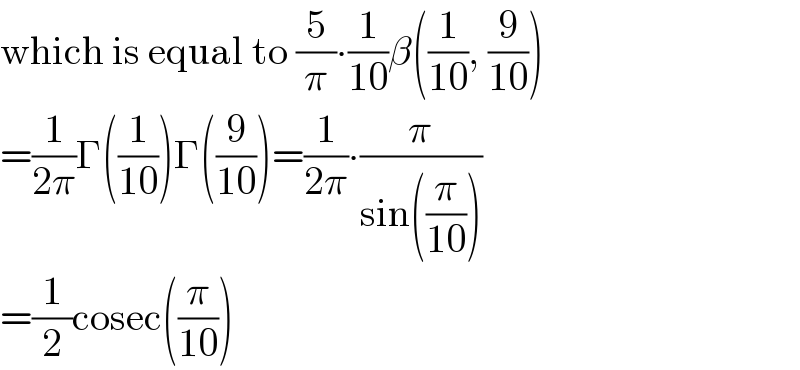
$$\mathrm{which}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\frac{\mathrm{5}}{\pi}\centerdot\frac{\mathrm{1}}{\mathrm{10}}\beta\left(\frac{\mathrm{1}}{\mathrm{10}},\:\frac{\mathrm{9}}{\mathrm{10}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi}\Gamma\left(\frac{\mathrm{1}}{\mathrm{10}}\right)\Gamma\left(\frac{\mathrm{9}}{\mathrm{10}}\right)=\frac{\mathrm{1}}{\mathrm{2}\pi}\centerdot\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{10}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cosec}\left(\frac{\pi}{\mathrm{10}}\right) \\ $$
