
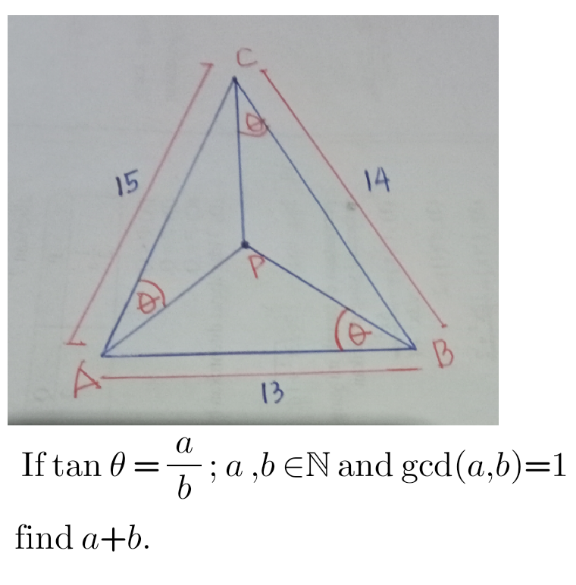
Question Number 189921 by cortano12 last updated on 26/Mar/23
Commented by nikif99 last updated on 25/Mar/23
Commented by cortano12 last updated on 26/Mar/23

$$\mathrm{i}\:\mathrm{have}\:\mathrm{corrected}\:\mathrm{the}\:\mathrm{question}\: \\ $$
Answered by nikif99 last updated on 25/Mar/23
![PD⊥BC ⇒CD=7 ⇒CP=d=(7/(cos θ)) (1) △ABC: cos C=((AC^2 +BC^2 −AB^2 )/(2∙AC∙BC))=0.6 ⇒sin C=0.8 ∡ω=360−∡CPB−∡BPA= 360−(180−2θ)−[180−(∡A−θ)−(∡B−θ)]= 360−180+2θ−180+∡A−θ+∡B−θ ⇒ ∡ω=∡A+∡B=180−∡C △ACP: (d/(sin θ))=((AC)/(sin ω))=((15)/(sin ∡C))=((15)/(0.8))⇒ (d/(sin θ))=18.75 (2) (1)(2) ⇒(7/(cos θ sin θ))=18.75 ⇒((14)/(2 cos θ sin θ))=18.75 ⇒ sin (2θ)=((14)/(18.75)) ⇒2θ=48.302 and θ=24.151 ⇒tan θ=0.448395=(a/b) Then by computer aided program, reached a=908, b=2025 and a+b=2933](Q189999.png)
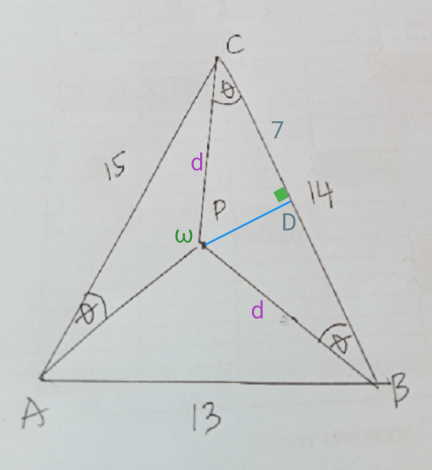
$${PD}\bot{BC}\:\Rightarrow{CD}=\mathrm{7}\:\Rightarrow{CP}={d}=\frac{\mathrm{7}}{\mathrm{cos}\:\theta}\:\left(\mathrm{1}\right) \\ $$$$\bigtriangleup{ABC}:\:\mathrm{cos}\:{C}=\frac{{AC}^{\mathrm{2}} +{BC}^{\mathrm{2}} −{AB}^{\mathrm{2}} }{\mathrm{2}\centerdot{AC}\centerdot{BC}}=\mathrm{0}.\mathrm{6}\:\Rightarrow\mathrm{sin}\:{C}=\mathrm{0}.\mathrm{8} \\ $$$$\measuredangle\omega=\mathrm{360}−\measuredangle{CPB}−\measuredangle{BPA}= \\ $$$$\mathrm{360}−\left(\mathrm{180}−\mathrm{2}\theta\right)−\left[\mathrm{180}−\left(\measuredangle{A}−\theta\right)−\left(\measuredangle{B}−\theta\right)\right]= \\ $$$$\mathrm{360}−\mathrm{180}+\mathrm{2}\theta−\mathrm{180}+\measuredangle{A}−\theta+\measuredangle{B}−\theta\:\Rightarrow \\ $$$$\measuredangle\omega=\measuredangle{A}+\measuredangle{B}=\mathrm{180}−\measuredangle{C} \\ $$$$\bigtriangleup{ACP}:\:\frac{{d}}{\mathrm{sin}\:\theta}=\frac{{AC}}{\mathrm{sin}\:\omega}=\frac{\mathrm{15}}{\mathrm{sin}\:\measuredangle{C}}=\frac{\mathrm{15}}{\mathrm{0}.\mathrm{8}}\Rightarrow \\ $$$$\frac{{d}}{\mathrm{sin}\:\theta}=\mathrm{18}.\mathrm{75}\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\left(\mathrm{2}\right)\:\Rightarrow\frac{\mathrm{7}}{\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta}=\mathrm{18}.\mathrm{75}\:\Rightarrow\frac{\mathrm{14}}{\mathrm{2}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta}=\mathrm{18}.\mathrm{75}\:\Rightarrow \\ $$$$\mathrm{sin}\:\left(\mathrm{2}\theta\right)=\frac{\mathrm{14}}{\mathrm{18}.\mathrm{75}}\:\Rightarrow\mathrm{2}\theta=\mathrm{48}.\mathrm{302} \\ $$$${and}\:\theta=\mathrm{24}.\mathrm{151}\:\Rightarrow\mathrm{tan}\:\theta=\mathrm{0}.\mathrm{448395}=\frac{{a}}{{b}} \\ $$$${Then}\:{by}\:{computer}\:{aided}\:{program}, \\ $$$${reached}\:{a}=\mathrm{908},\:{b}=\mathrm{2025}\:{and}\:{a}+{b}=\mathrm{2933} \\ $$
Answered by mr W last updated on 18/Nov/23

$${s}=\frac{\mathrm{13}+\mathrm{14}+\mathrm{15}}{\mathrm{2}}=\mathrm{21} \\ $$$$\left.\Delta=\sqrt{\mathrm{21}×\left(\mathrm{21}−\mathrm{13}\right)\left(\mathrm{21}−\mathrm{14}\right)\left(\mathrm{21}−\mathrm{15}\right.}\right)=\mathrm{84} \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{4}×\mathrm{84}}{\mathrm{13}^{\mathrm{2}} +\mathrm{14}^{\mathrm{2}} +\mathrm{15}^{\mathrm{2}} }=\frac{\mathrm{168}}{\mathrm{295}}=\frac{{a}}{{b}} \\ $$$$\Rightarrow{a}+{b}=\mathrm{168}+\mathrm{295}=\mathrm{463}\:\checkmark \\ $$
Commented by mr W last updated on 18/Nov/23

$${formula}\:{see}\:{Q}#\mathrm{198913} \\ $$
