
Question Number 189858 by Shrinava last updated on 23/Mar/23
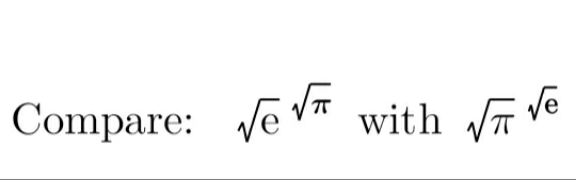
Answered by mr W last updated on 23/Mar/23
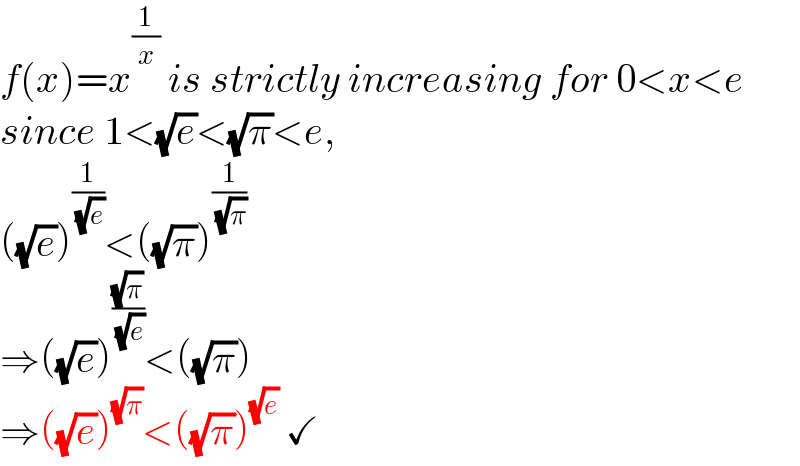
$${f}\left({x}\right)={x}^{\frac{\mathrm{1}}{{x}}} \:{is}\:{strictly}\:{increasing}\:{for}\:\mathrm{0}<{x}<{e} \\ $$$${since}\:\mathrm{1}<\sqrt{{e}}<\sqrt{\pi}<{e}, \\ $$$$\left(\sqrt{{e}}\right)^{\frac{\mathrm{1}}{\:\sqrt{{e}}}} <\left(\sqrt{\pi}\right)^{\frac{\mathrm{1}}{\:\sqrt{\pi}}} \\ $$$$\Rightarrow\left(\sqrt{{e}}\right)^{\frac{\sqrt{\pi}}{\:\sqrt{{e}}}} <\left(\sqrt{\pi}\right) \\ $$$$\Rightarrow\left(\sqrt{{e}}\right)^{\sqrt{\pi}} <\left(\sqrt{\pi}\right)^{\sqrt{{e}}} \:\checkmark \\ $$
Commented by Shrinava last updated on 24/Mar/23
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor} \\ $$
