
Question Number 189715 by Rupesh123 last updated on 20/Mar/23
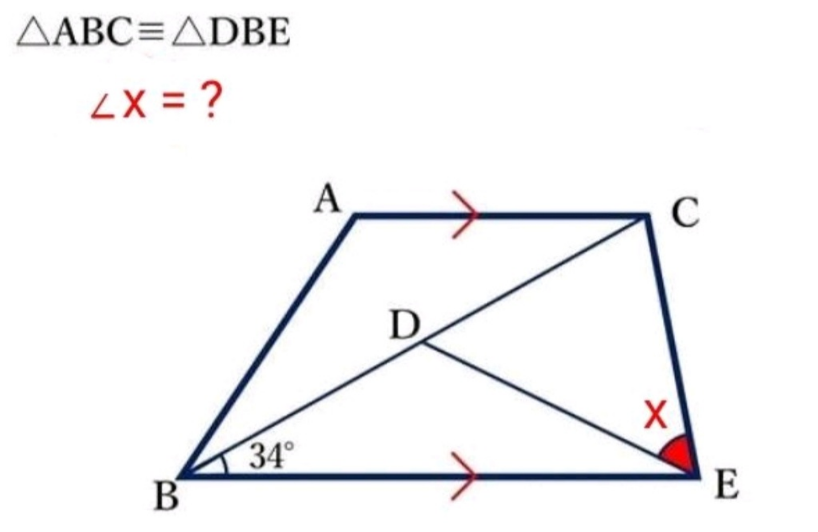
Answered by som(math1967) last updated on 21/Mar/23
![△ABC≅△DBE ⇒AB=DB BC=BE ⇒∠BEC=∠BCE ∠ACB=34 [∠ACB=∠CBE] ∠DEB=∠ACB=34 AC∥BE ∠ACE+∠BEC=180 34+x+x+34+34=180 2x=180−102 x=39](Q189723.png)
$$\bigtriangleup{ABC}\cong\bigtriangleup{DBE} \\ $$$$\Rightarrow{AB}={DB} \\ $$$${BC}={BE}\:\Rightarrow\angle{BEC}=\angle{BCE} \\ $$$$\angle{ACB}=\mathrm{34}\:\left[\angle{ACB}=\angle{CBE}\right]\:\: \\ $$$$\angle{DEB}=\angle{ACB}=\mathrm{34} \\ $$$${AC}\parallel{BE}\:\:\angle{ACE}+\angle{BEC}=\mathrm{180} \\ $$$$\mathrm{34}+{x}+{x}+\mathrm{34}+\mathrm{34}=\mathrm{180} \\ $$$$\mathrm{2}{x}=\mathrm{180}−\mathrm{102} \\ $$$${x}=\mathrm{39} \\ $$
Commented by Rupesh123 last updated on 21/Mar/23
Triangle ABC = Triangle DBE it implies that AB= DE, why?
Commented by som(math1967) last updated on 28/Mar/23
![AB=DB [corresponding part of congruence triangle]](Q190142.png)
$${AB}={DB}\:\left[{corresponding}\:{part}\right. \\ $$$$\left.{of}\:{congruence}\:{triangle}\right] \\ $$
