
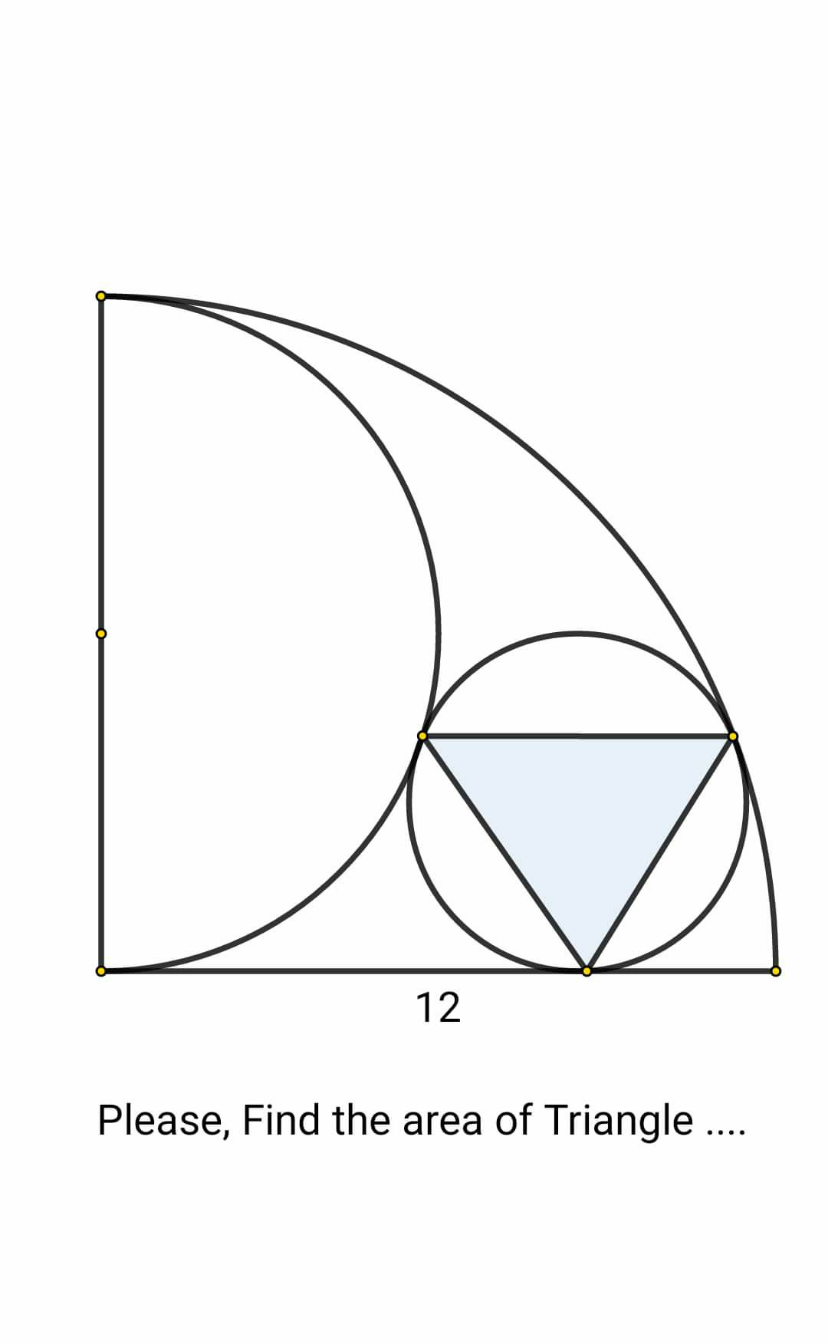
Question Number 189535 by normans last updated on 18/Mar/23
Answered by mr W last updated on 18/Mar/23
Commented by mr W last updated on 18/Mar/23
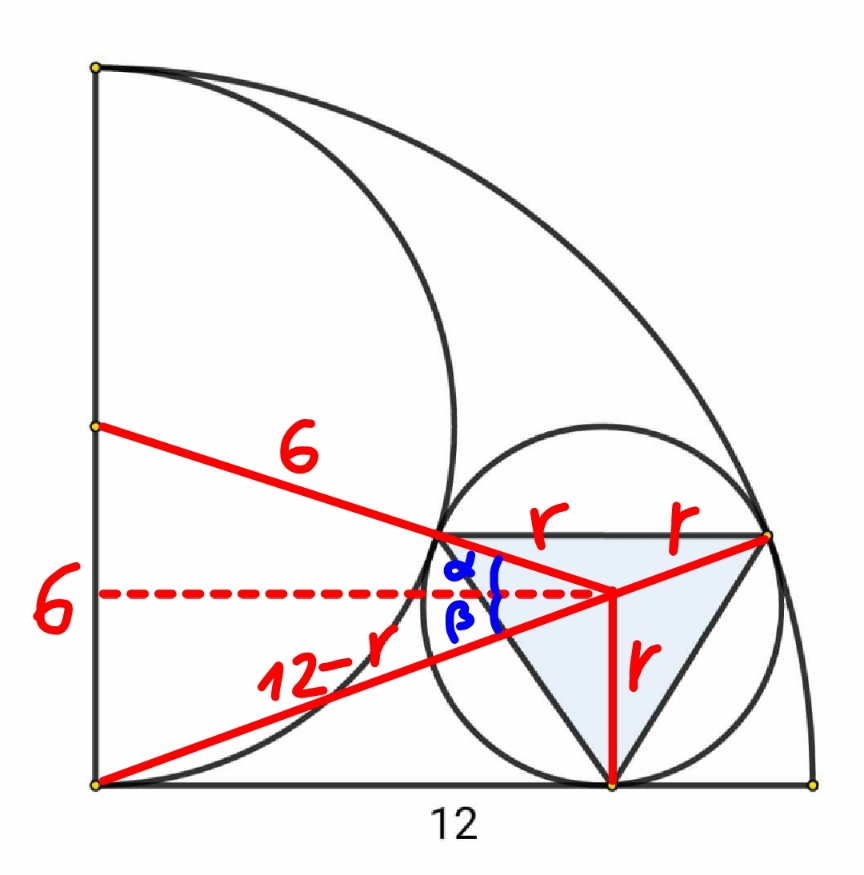
![(12−r)^2 −r^2 =(6+r)^2 −(6−r)^2 ⇒r=3 sin α=sin β=(3/9)=(1/3) A_(shaded) =(r^2 /2)[sin (90°+α)+sin (180°−α−β)+sin (90°+β)] =(r^2 /2)(2 cos α+sin 2α) =cos α (1+sin α)r^2 =((2(√2))/3) (1+(1/3))×3^2 =8(√2) ✓](Q189548.png)
$$\left(\mathrm{12}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} =\left(\mathrm{6}+{r}\right)^{\mathrm{2}} −\left(\mathrm{6}−{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\mathrm{3} \\ $$$$\mathrm{sin}\:\alpha=\mathrm{sin}\:\beta=\frac{\mathrm{3}}{\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${A}_{{shaded}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{sin}\:\left(\mathrm{90}°+\alpha\right)+\mathrm{sin}\:\left(\mathrm{180}°−\alpha−\beta\right)+\mathrm{sin}\:\left(\mathrm{90}°+\beta\right)\right] \\ $$$$\:=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\:\mathrm{cos}\:\alpha+\mathrm{sin}\:\mathrm{2}\alpha\right) \\ $$$$\:=\mathrm{cos}\:\alpha\:\left(\mathrm{1}+\mathrm{sin}\:\alpha\right){r}^{\mathrm{2}} \\ $$$$\:=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)×\mathrm{3}^{\mathrm{2}} \\ $$$$\:=\mathrm{8}\sqrt{\mathrm{2}}\:\checkmark \\ $$
