Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 189429 by 073 last updated on 16/Mar/23

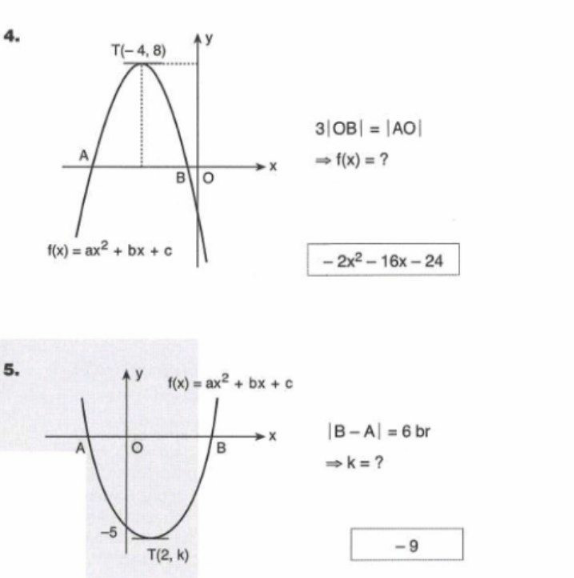
Commented by 073 last updated on 16/Mar/23

solution please

$$\mathrm{solution}\:\mathrm{please} \\ $$

Answered by cortano12 last updated on 16/Mar/23

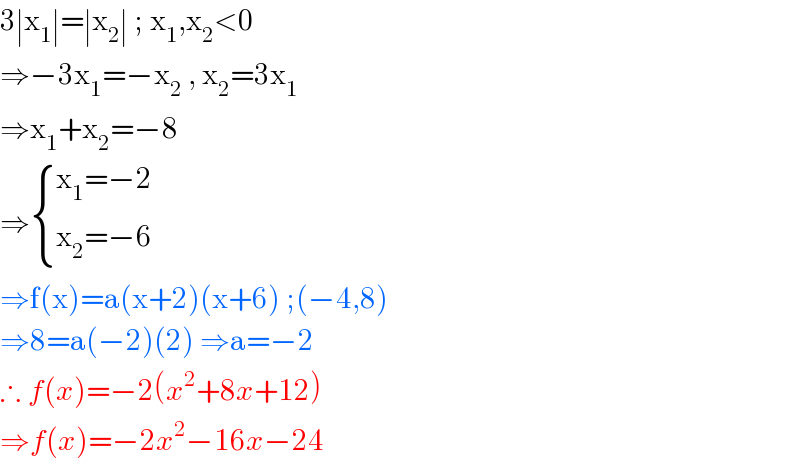
3∣x_1 ∣=∣x_2 ∣ ; x_1 ,x_2 <0 ⇒−3x_1 =−x_2 , x_2 =3x_1 ⇒x_1 +x_2 =−8 ⇒ { ((x_1 =−2)),((x_2 =−6)) :} ⇒f(x)=a(x+2)(x+6) ;(−4,8) ⇒8=a(−2)(2) ⇒a=−2 ∴ f(x)=−2(x^2 +8x+12) ⇒f(x)=−2x^2 −16x−24

$$\mathrm{3}\mid\mathrm{x}_{\mathrm{1}} \mid=\mid\mathrm{x}_{\mathrm{2}} \mid\:;\:\mathrm{x}_{\mathrm{1}} ,\mathrm{x}_{\mathrm{2}} <\mathrm{0} \\ $$$$\Rightarrow−\mathrm{3x}_{\mathrm{1}} =−\mathrm{x}_{\mathrm{2}} \:,\:\mathrm{x}_{\mathrm{2}} =\mathrm{3x}_{\mathrm{1}} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} =−\mathrm{8} \\ $$$$\Rightarrow\begin{cases}{\mathrm{x}_{\mathrm{1}} =−\mathrm{2}}\\{\mathrm{x}_{\mathrm{2}} =−\mathrm{6}}\end{cases} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{a}\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{6}\right)\:;\left(−\mathrm{4},\mathrm{8}\right) \\ $$$$\Rightarrow\mathrm{8}=\mathrm{a}\left(−\mathrm{2}\right)\left(\mathrm{2}\right)\:\Rightarrow\mathrm{a}=−\mathrm{2} \\ $$$$\therefore\:{f}\left({x}\right)=−\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{12}\right) \\ $$$$\Rightarrow{f}\left({x}\right)=−\mathrm{2}{x}^{\mathrm{2}} −\mathrm{16}{x}−\mathrm{24} \\ $$

Commented by 073 last updated on 16/Mar/23

nice solution thanks alot please another one

$$\mathrm{nice}\:\mathrm{solution} \\ $$$$\mathrm{thanks}\:\mathrm{alot} \\ $$$$\mathrm{please}\:\mathrm{another}\:\mathrm{one} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com