Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

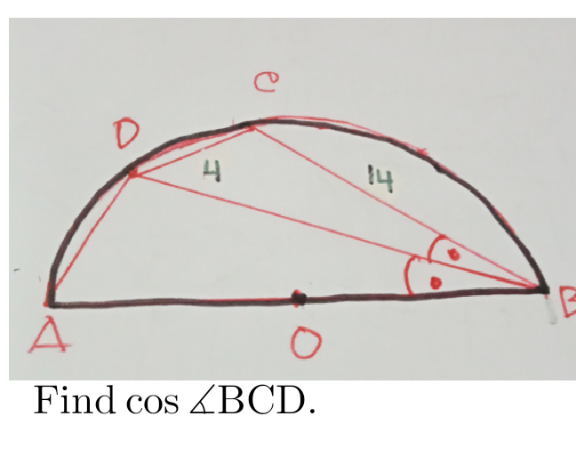
Question Number 189339 by cortano12 last updated on 15/Mar/23

Answered by HeferH last updated on 15/Mar/23

Commented by HeferH last updated on 15/Mar/23

cos (90°+α)=? 8∙4 = (x+14)x x=2 sin α = (4/(16)) = (1/4) α = sin^(−1) ((1/4)) ≈ 14.4° cos (104.4°°) ≈ −0.24

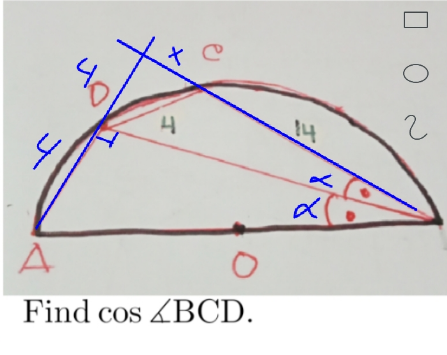
$$\:\mathrm{cos}\:\left(\mathrm{90}°+\alpha\right)=? \\ $$$$\:\mathrm{8}\centerdot\mathrm{4}\:=\:\left(\mathrm{x}+\mathrm{14}\right)\mathrm{x} \\ $$$$\:\mathrm{x}=\mathrm{2} \\ $$$$\:\mathrm{sin}\:\:\alpha\:=\:\frac{\mathrm{4}}{\mathrm{16}}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\: \\ $$$$\:\alpha\:=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:\approx\:\:\mathrm{14}.\mathrm{4}° \\ $$$$\:\mathrm{cos}\:\left(\mathrm{104}.\mathrm{4}°°\right)\:\approx\:−\mathrm{0}.\mathrm{24} \\ $$

Commented by cortano12 last updated on 15/Mar/23

why sin α=(4/(16))=(1/2) ?

$$\mathrm{why}\:\mathrm{sin}\:\alpha=\frac{\mathrm{4}}{\mathrm{16}}=\frac{\mathrm{1}}{\mathrm{2}}\:? \\ $$

Commented by HeferH last updated on 15/Mar/23

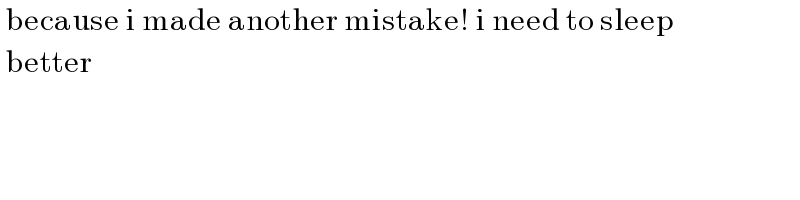
because i made another mistake! i need to sleep better

$$\:\mathrm{because}\:\mathrm{i}\:\mathrm{made}\:\mathrm{another}\:\mathrm{mistake}!\:\mathrm{i}\:\mathrm{need}\:\mathrm{to}\:\mathrm{sleep} \\ $$$$\:\mathrm{better}\: \\ $$

Commented by cortano12 last updated on 15/Mar/23

my solution ⇒sin α=(4/(2r)) = (2/r) ⇒cos 2α=((14)/(2r))=(7/r) ⇒1−2sin^2 α=(7/r) ⇒1−(8/r^2 ) =(7/r) ; r^2 −7r−8=0 ⇒(r−8)(r+1)=0 ; r=8 BD=(√(16^2 −4^2 )) =(√(20.12))=4(√(15)) ⇒cos ∡BCD=((16+196−240)/(2.4.14)) ⇒cos ∡BCD=−((28)/(4.28))=−(1/4)

$$\mathrm{my}\:\mathrm{solution} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{4}}{\mathrm{2r}}\:=\:\frac{\mathrm{2}}{\mathrm{r}} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2}\alpha=\frac{\mathrm{14}}{\mathrm{2r}}=\frac{\mathrm{7}}{\mathrm{r}} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \alpha=\frac{\mathrm{7}}{\mathrm{r}} \\ $$$$\Rightarrow\mathrm{1}−\frac{\mathrm{8}}{\mathrm{r}^{\mathrm{2}} }\:=\frac{\mathrm{7}}{\mathrm{r}}\:;\:\mathrm{r}^{\mathrm{2}} −\mathrm{7r}−\mathrm{8}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{r}−\mathrm{8}\right)\left(\mathrm{r}+\mathrm{1}\right)=\mathrm{0}\:;\:\mathrm{r}=\mathrm{8} \\ $$$$\mathrm{BD}=\sqrt{\mathrm{16}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }\:=\sqrt{\mathrm{20}.\mathrm{12}}=\mathrm{4}\sqrt{\mathrm{15}} \\ $$$$\:\Rightarrow\mathrm{cos}\:\measuredangle\mathrm{BCD}=\frac{\mathrm{16}+\mathrm{196}−\mathrm{240}}{\mathrm{2}.\mathrm{4}.\mathrm{14}} \\ $$$$\Rightarrow\mathrm{cos}\:\measuredangle\mathrm{BCD}=−\frac{\mathrm{28}}{\mathrm{4}.\mathrm{28}}=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Commented by HeferH last updated on 15/Mar/23

👏

👏

Terms of Service

Privacy Policy

Contact: info@tinkutara.com