
Question Number 189293 by Rupesh123 last updated on 14/Mar/23
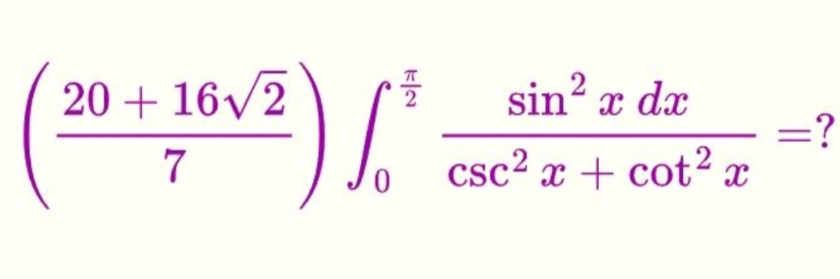
Answered by Sutrisno last updated on 14/Mar/23
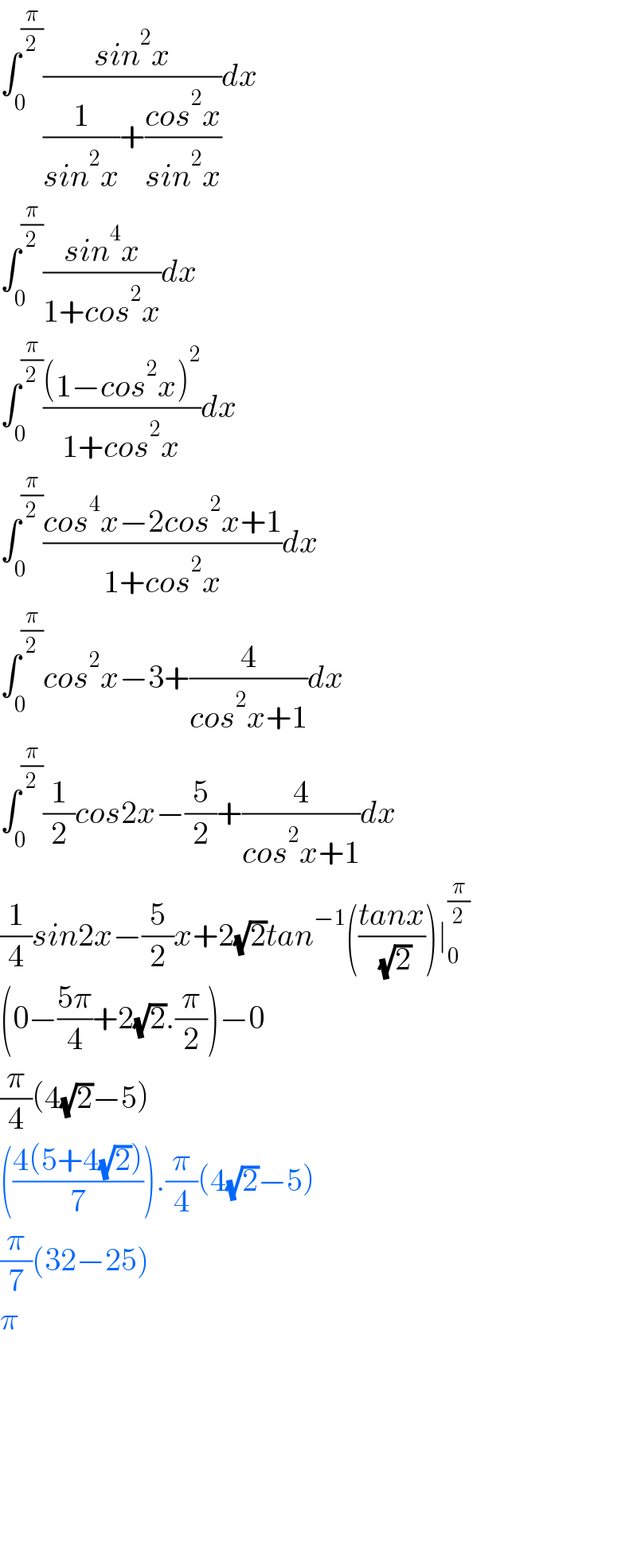
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}} {x}}{\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {x}}+\frac{{cos}^{\mathrm{2}} {x}}{{sin}^{\mathrm{2}} {x}}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{4}} {x}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{\mathrm{1}+{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{4}} {x}−\mathrm{2}{cos}^{\mathrm{2}} {x}+\mathrm{1}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}} {x}−\mathrm{3}+\frac{\mathrm{4}}{{cos}^{\mathrm{2}} {x}+\mathrm{1}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{2}{x}−\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{4}}{{cos}^{\mathrm{2}} {x}+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{2}{x}−\frac{\mathrm{5}}{\mathrm{2}}{x}+\mathrm{2}\sqrt{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\frac{{tanx}}{\:\sqrt{\mathrm{2}}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\left(\mathrm{0}−\frac{\mathrm{5}\pi}{\mathrm{4}}+\mathrm{2}\sqrt{\mathrm{2}}.\frac{\pi}{\mathrm{2}}\right)−\mathrm{0} \\ $$$$\frac{\pi}{\mathrm{4}}\left(\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{5}\right) \\ $$$$\left(\frac{\mathrm{4}\left(\mathrm{5}+\mathrm{4}\sqrt{\mathrm{2}}\right)}{\mathrm{7}}\right).\frac{\pi}{\mathrm{4}}\left(\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{5}\right) \\ $$$$\frac{\pi}{\mathrm{7}}\left(\mathrm{32}−\mathrm{25}\right) \\ $$$$\pi \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
