
Question Number 189267 by Rupesh123 last updated on 14/Mar/23
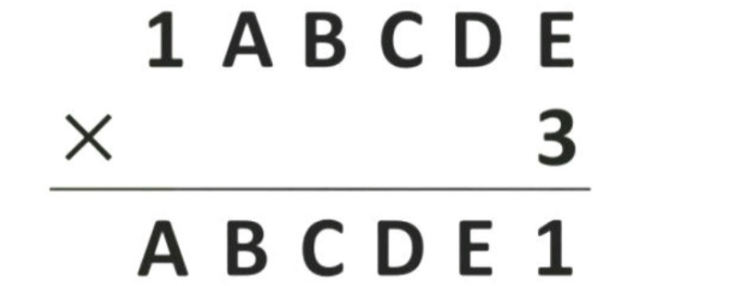
Commented by Rupesh123 last updated on 14/Mar/23
Find the 5-digit number ABCDE such that
Answered by HeferH last updated on 14/Mar/23

$$\:\bullet\:\mathrm{E}\:=\:\mathrm{7} \\ $$$$\:\bullet\:\mathrm{3D}\:+\:\mathrm{2}\:=\:\mathrm{X7} \\ $$$$\:\mathrm{X}\:=\:\mathrm{1};\:\mathrm{D}\:=\:\mathrm{5} \\ $$$$\:\bullet\:\mathrm{3C}\:+\:\mathrm{1}\:=\:\mathrm{Y5} \\ $$$$\:\mathrm{Y}\:=\:\mathrm{2};\:\mathrm{C}\:=\:\mathrm{8}\: \\ $$$$\:\bullet\:\mathrm{3B}\:+\:\mathrm{2}\:=\:\mathrm{Z8} \\ $$$$\:\mathrm{Z}\:=\:\mathrm{0};\:\mathrm{B}\:=\:\mathrm{2} \\ $$$$\:\bullet\:\mathrm{3A}\:=\:\mathrm{M2} \\ $$$$\:\mathrm{M}\:=\:\mathrm{1};\:\mathrm{A}\:=\:\mathrm{4} \\ $$$$\:\mathrm{ABCDE}\:=\:\mathrm{42857}\: \\ $$
Commented by Rupesh123 last updated on 14/Mar/23
Excellent
Answered by manxsol last updated on 14/Mar/23
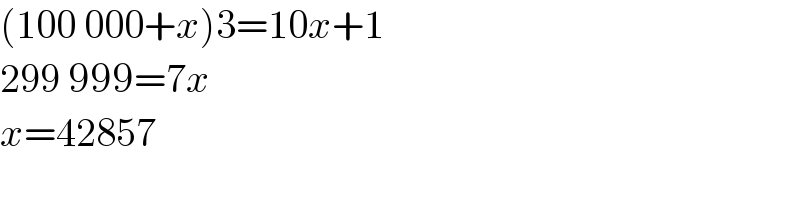
$$\left(\mathrm{100}\:\mathrm{000}+{x}\right)\mathrm{3}=\mathrm{10}{x}+\mathrm{1} \\ $$$$\mathrm{299}\:\mathrm{999}=\mathrm{7}{x} \\ $$$${x}=\mathrm{42857} \\ $$
Commented by HeferH last updated on 14/Mar/23

$$\left.\mathrm{excelente}\:\:\mathrm{solucion}\::\right) \\ $$
Commented by Rasheed.Sindhi last updated on 14/Mar/23

$$\mathbb{T}\boldsymbol{\mathrm{he}}\:\boldsymbol{\mathrm{smartest}}\:\boldsymbol{\mathrm{possible}}\:\boldsymbol{\mathrm{solution}}! \\ $$
Commented by Rupesh123 last updated on 14/Mar/23
Excellent
Answered by mr W last updated on 14/Mar/23

$$\left(\mathrm{1}\boldsymbol{{abcdef}}...\boldsymbol{{uvw}}\right)×\mathrm{3}=\left(\boldsymbol{{abcdef}}...\boldsymbol{{uvw}}\mathrm{1}\right) \\ $$$${say}\:\boldsymbol{{abcdef}}...\boldsymbol{{uvw}}\:{is}\:{a}\:\boldsymbol{{n}}\:{digit}\:{number}\:\boldsymbol{{x}}. \\ $$$$\left(\mathrm{10}^{{n}} +{x}\right)×\mathrm{3}=\mathrm{10}{x}+\mathrm{1} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}×\mathrm{10}^{{n}} −\mathrm{1}}{\mathrm{7}} \\ $$$${n}=\mathrm{5}:\:{x}=\mathrm{42857} \\ $$$${n}=\mathrm{11}:\:{x}=\mathrm{42857142857} \\ $$$${n}=\mathrm{17}:\:{x}=\mathrm{42857142857142857} \\ $$$${n}=\mathrm{23}:\:{x}=\mathrm{42857142857142857142857} \\ $$$$.... \\ $$$${generally}\: \\ $$$${x}=\frac{\mathrm{3}×\mathrm{10}^{\mathrm{6}{k}−\mathrm{1}} −\mathrm{1}}{\mathrm{7}}=\mathrm{42857142857}...\mathrm{142857142857} \\ $$
Commented by mr W last updated on 14/Mar/23
$${see}\:{similar}\:{question}\:\mathrm{10521}. \\ $$
Commented by manxsol last updated on 14/Mar/23

$${Sir}.\:{W},\:{the}\:{question}\:{is} \\ $$$$\:{from}\:\mathrm{2017}\:{so}\:{there}\:{is} \\ $$$$\:{a}\:{question}\:{search}\:{engine}? \\ $$$$ \\ $$
Commented by mr W last updated on 14/Mar/23

$${yes},\:{there}\:{is}\:{a}\:{search}\:{engine}\:{in}\:{the} \\ $$$${app}.\:{but}\:{the}\:{search}\:{engine}\:{of}\:{the}\:{app} \\ $$$${is}\:{not}\:{so}\:{good}. \\ $$$${i}\:{made}\:{backups}\:{for}\:{some}\:{questions} \\ $$$${i}\:{solved}.\:{in}\:{current}\:{case}\:{i}\:{remember} \\ $$$${there}\:{was}\:{such}\:{a}\:{similar}\:{question}, \\ $$$${and}\:{could}\:{find}\:{it}\:{in}\:{my}\:{backups}. \\ $$
Commented by manxsol last updated on 14/Mar/23

$${I}\:{will}\:{also}\:{start}\:{indexing}. \\ $$$${I}\:{wanted}\:{to}\:\:{thank}\left[{you}\right. \\ $$$$\:{very}\:{interesting}\:{Mac}\:\:{Tutor} \\ $$$$\:{link}\:\left({number}\:{catalan}\right) \\ $$
Commented by mr W last updated on 14/Mar/23
$${nice}\:{to}\:{know}\:{that}\:{you}\:{like}\:{it}! \\ $$
