Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 189127 by Mingma last updated on 12/Mar/23

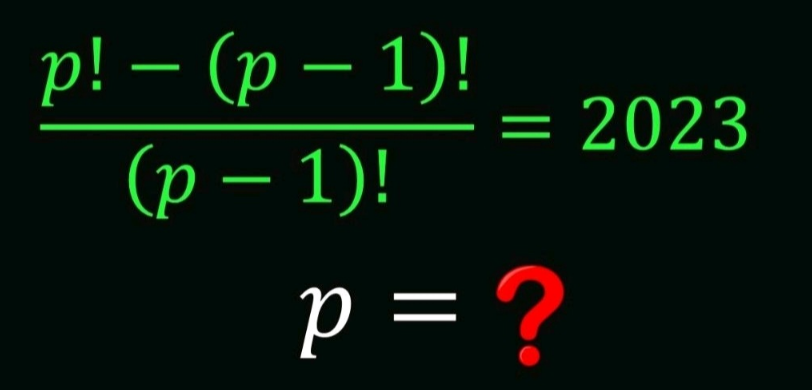
Answered by Rasheed.Sindhi last updated on 12/Mar/23

((p!−(p−1)!)/((p−1)!))=2023 (((p−1)![p−1])/((p−1)!))=2023 p−1=2023 p=2024

$$\frac{{p}!−\left({p}−\mathrm{1}\right)!}{\left({p}−\mathrm{1}\right)!}=\mathrm{2023} \\ $$$$\frac{\left({p}−\mathrm{1}\right)!\left[{p}−\mathrm{1}\right]}{\left({p}−\mathrm{1}\right)!}=\mathrm{2023} \\ $$$${p}−\mathrm{1}=\mathrm{2023} \\ $$$${p}=\mathrm{2024} \\ $$

Commented by Mingma last updated on 13/Mar/23

Excellent!

Answered by Rasheed.Sindhi last updated on 13/Mar/23

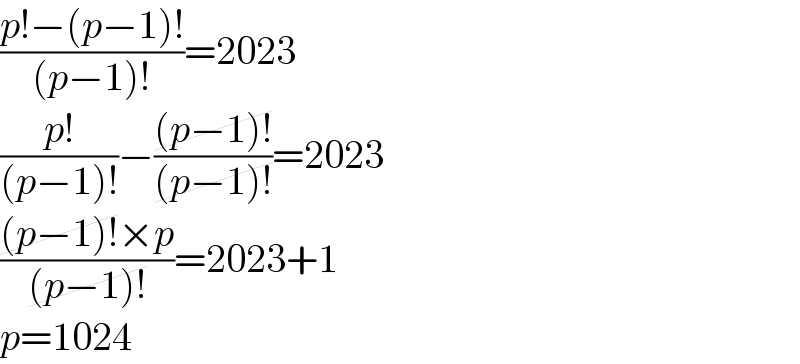
((p!−(p−1)!)/((p−1)!))=2023 ((p!)/((p−1)!))−(((p−1)!)/((p−1)!))=2023 (((p−1)!×p)/((p−1)!))=2023+1 p=1024

$$\frac{{p}!−\left({p}−\mathrm{1}\right)!}{\left({p}−\mathrm{1}\right)!}=\mathrm{2023} \\ $$$$\frac{{p}!}{\left({p}−\mathrm{1}\right)!}−\frac{\cancel{\left({p}−\mathrm{1}\right)!}}{\cancel{\left({p}−\mathrm{1}\right)!}}=\mathrm{2023} \\ $$$$\frac{\cancel{\left({p}−\mathrm{1}\right)!}×{p}}{\cancel{\left({p}−\mathrm{1}\right)!}}=\mathrm{2023}+\mathrm{1} \\ $$$${p}=\mathrm{1024} \\ $$

Answered by Rasheed.Sindhi last updated on 13/Mar/23

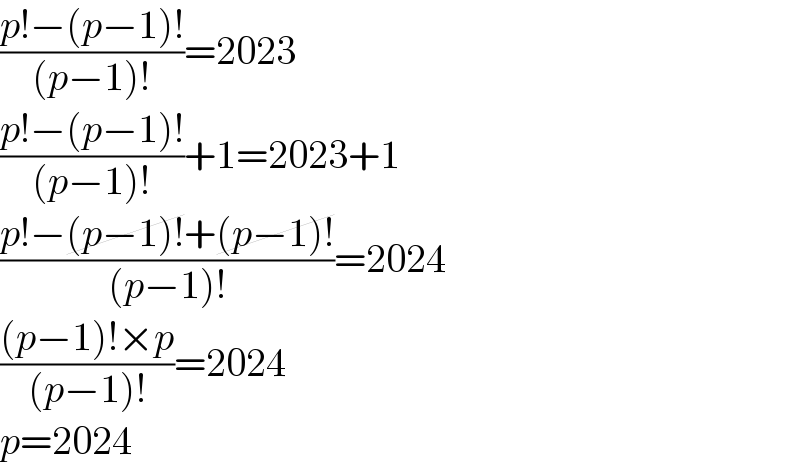
((p!−(p−1)!)/((p−1)!))=2023 ((p!−(p−1)!)/((p−1)!))+1=2023+1 ((p!−(p−1)!+(p−1)!)/((p−1)!))=2024 (((p−1)!×p)/((p−1)!))=2024 p=2024

$$\frac{{p}!−\left({p}−\mathrm{1}\right)!}{\left({p}−\mathrm{1}\right)!}=\mathrm{2023} \\ $$$$\frac{{p}!−\left({p}−\mathrm{1}\right)!}{\left({p}−\mathrm{1}\right)!}+\mathrm{1}=\mathrm{2023}+\mathrm{1} \\ $$$$\frac{{p}!−\cancel{\left({p}−\mathrm{1}\right)!}+\cancel{\left({p}−\mathrm{1}\right)!}}{\left({p}−\mathrm{1}\right)!}=\mathrm{2024} \\ $$$$\frac{\left({p}−\mathrm{1}\right)!×{p}}{\left({p}−\mathrm{1}\right)!}=\mathrm{2024} \\ $$$${p}=\mathrm{2024} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com