
Question Number 189126 by Mingma last updated on 12/Mar/23
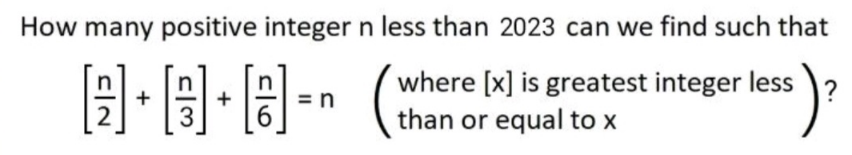
Answered by mr W last updated on 12/Mar/23

$${if}\:\mathrm{6}{k}\leqslant{n}<\mathrm{6}{k}+\mathrm{2}: \\ $$$$\mathrm{3}{k}+\mathrm{2}{k}+{k}={n}\:\Rightarrow{n}=\mathrm{6}{k}\:\checkmark \\ $$$${if}\:\mathrm{6}{k}+\mathrm{2}\leqslant{n}<\mathrm{6}{k}+\mathrm{3}: \\ $$$$\mathrm{3}{k}+\mathrm{1}+\mathrm{2}{k}+{k}={n}\:\Rightarrow{n}=\mathrm{6}{k}+\mathrm{1}\:\rightarrow{bad} \\ $$$${if}\:\mathrm{6}{k}+\mathrm{3}\leqslant{n}<\mathrm{6}{k}+\mathrm{4}: \\ $$$$\mathrm{3}{k}+\mathrm{1}+\mathrm{2}{k}+\mathrm{1}+{k}={n}\:\Rightarrow{n}=\mathrm{6}{k}+\mathrm{2}\:\rightarrow{bad} \\ $$$${if}\:\mathrm{6}{k}+\mathrm{4}\leqslant{n}<\mathrm{6}{k}+\mathrm{6}: \\ $$$$\mathrm{3}{k}+\mathrm{2}+\mathrm{2}{k}+\mathrm{1}+{k}={n}\:\Rightarrow{n}=\mathrm{6}{k}+\mathrm{3}\:\rightarrow{bad} \\ $$$${that}\:{means}\:{the}\:{general}\:{solution}\:{is} \\ $$$${n}=\mathrm{6}{k}\:{with}\:{k}\in{Z} \\ $$$${for}\:\mathrm{0}<{n}<\mathrm{2023}\:{there}\:{are}\:\mathrm{337}\:{integers}: \\ $$$${n}=\mathrm{6},\mathrm{12},\mathrm{18},...,\mathrm{2016},\mathrm{2022} \\ $$
Commented by Mingma last updated on 13/Mar/23
Excellent!
