
Question Number 189123 by Rupesh123 last updated on 12/Mar/23
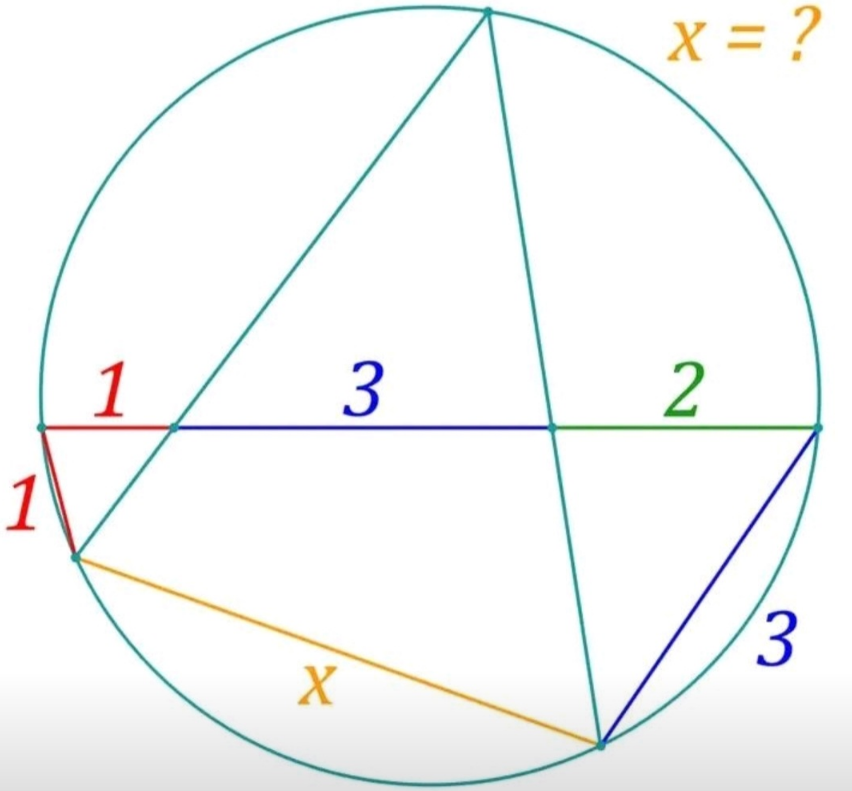
Answered by mr W last updated on 13/Mar/23
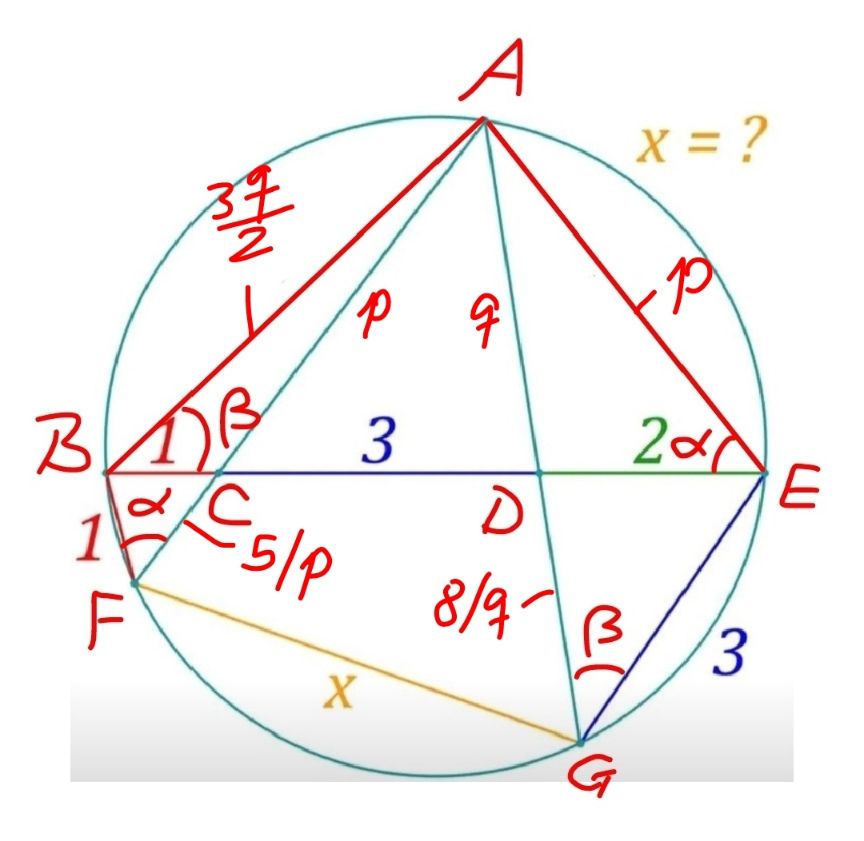
Commented by mr W last updated on 13/Mar/23

$${let}\:{AC}={p},\:{AD}={q} \\ $$$$\frac{{AE}}{{BF}}=\frac{{AC}}{{BC}}=\frac{{CE}}{{CF}} \\ $$$$\frac{{AE}}{\mathrm{1}}=\frac{{p}}{\mathrm{1}}=\frac{\mathrm{5}}{{CF}} \\ $$$$\:\Rightarrow{AE}={p},\:{CF}=\frac{\mathrm{5}}{{p}} \\ $$$${similarly} \\ $$$$\Rightarrow{AB}=\frac{\mathrm{3}{q}}{\mathrm{2}},\:{DG}=\frac{\mathrm{8}}{{q}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{2}^{\mathrm{2}} +{p}^{\mathrm{2}} −{q}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}×{p}}=\frac{\mathrm{6}^{\mathrm{2}} +{p}^{\mathrm{2}} −\left(\frac{\mathrm{3}{q}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{6}×{p}} \\ $$$$\Rightarrow\mathrm{8}{p}^{\mathrm{2}} −\mathrm{3}{q}^{\mathrm{2}} =\mathrm{96}\:\:\:...\left({i}\right) \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{1}^{\mathrm{2}} +\left(\frac{\mathrm{3}{q}}{\mathrm{2}}\right)^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{2}×\mathrm{1}×\frac{\mathrm{3}{q}}{\mathrm{2}}}=\frac{\mathrm{6}^{\mathrm{2}} +\left(\frac{\mathrm{3}{q}}{\mathrm{2}}\right)^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{2}×\mathrm{6}×\frac{\mathrm{3}{q}}{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{9}{q}^{\mathrm{2}} −\mathrm{4}{p}^{\mathrm{2}} =\mathrm{24}\:\:\:...\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\Rightarrow{p}^{\mathrm{2}} =\frac{\mathrm{78}}{\mathrm{5}},\:{q}^{\mathrm{2}} =\frac{\mathrm{48}}{\mathrm{5}} \\ $$$$\frac{{x}^{\mathrm{2}} −\left({p}+\frac{\mathrm{5}}{{p}}\right)^{\mathrm{2}} −\left({q}+\frac{\mathrm{8}}{{q}}\right)^{\mathrm{2}} }{\mathrm{2}×\left({p}+\frac{\mathrm{5}}{{p}}\right)\left({q}+\frac{\mathrm{8}}{{q}}\right)}=\frac{\mathrm{3}^{\mathrm{2}} −{p}^{\mathrm{2}} −{q}^{\mathrm{2}} }{\mathrm{2}×{p}×{q}} \\ $$$${x}^{\mathrm{2}} =\mathrm{26}+{p}^{\mathrm{2}} +\frac{\mathrm{25}}{{p}^{\mathrm{2}} }+{q}^{\mathrm{2}} +\frac{\mathrm{64}}{{q}^{\mathrm{2}} }+\left(\mathrm{9}−{p}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{5}}{{p}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{8}}{{q}^{\mathrm{2}} }\right) \\ $$$${x}^{\mathrm{2}} =\mathrm{26}+\frac{\mathrm{78}}{\mathrm{5}}+\frac{\mathrm{25}×\mathrm{5}}{\mathrm{78}}+\frac{\mathrm{48}}{\mathrm{5}}+\frac{\mathrm{64}×\mathrm{5}}{\mathrm{48}}+\left(\mathrm{9}−\frac{\mathrm{78}}{\mathrm{5}}−\frac{\mathrm{48}}{\mathrm{5}}\right)\left(\mathrm{1}+\frac{\mathrm{5}×\mathrm{5}}{\mathrm{78}}\right)\left(\mathrm{1}+\frac{\mathrm{8}×\mathrm{5}}{\mathrm{48}}\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{81}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{9}}{\mathrm{2}}=\mathrm{4}.\mathrm{5}\:\checkmark \\ $$
Commented by Rupesh123 last updated on 14/Mar/23
Excellent!
Answered by HeferH last updated on 13/Mar/23

$$\mathrm{4}.\mathrm{5} \\ $$
Commented by mr W last updated on 13/Mar/23
$${i}\:{made}\:{some}\:{mistakes}.\:{it}'{s}\:{fixed}. \\ $$
Commented by Rupesh123 last updated on 13/Mar/23
Can you show workings?
Commented by HeferH last updated on 13/Mar/23
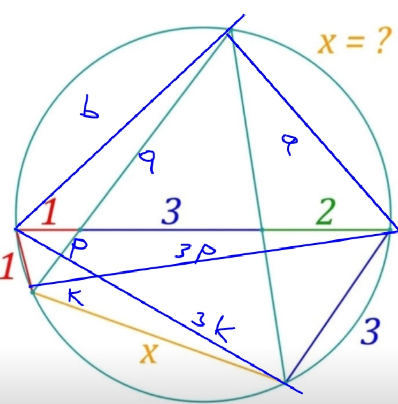
Commented by HeferH last updated on 13/Mar/23

Commented by HeferH last updated on 13/Mar/23

$$\mathrm{Im}\:\mathrm{sorry}\:\mathrm{if}\:\mathrm{there}\:\mathrm{is}\:\mathrm{any}\:\mathrm{error} \\ $$
