
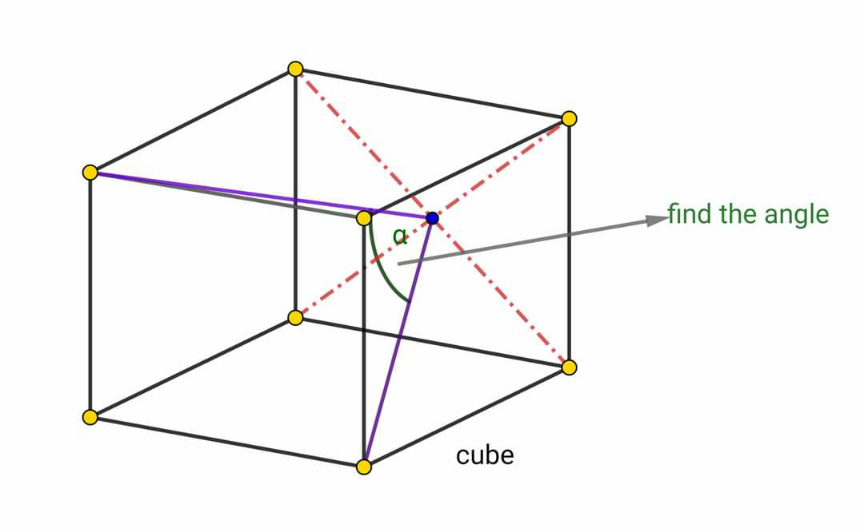
Question Number 188965 by normans last updated on 09/Mar/23
Answered by mr W last updated on 09/Mar/23
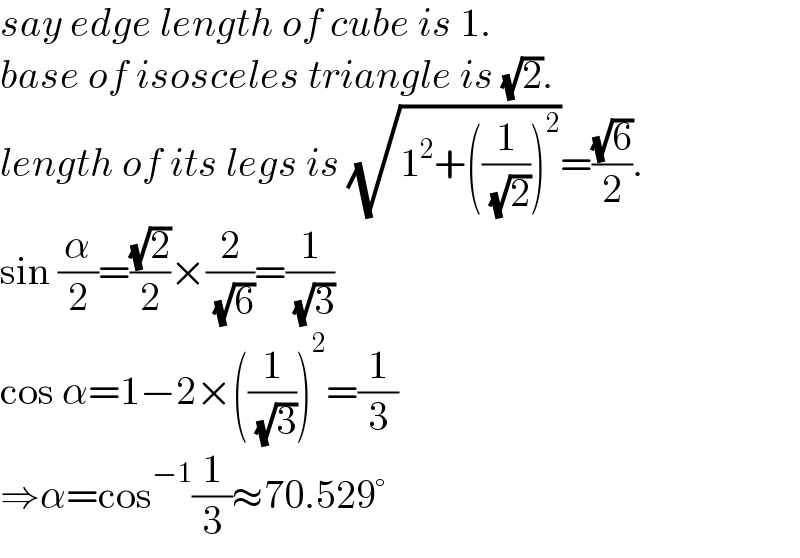
$${say}\:{edge}\:{length}\:{of}\:{cube}\:{is}\:\mathrm{1}. \\ $$$${base}\:{of}\:{isosceles}\:{triangle}\:{is}\:\sqrt{\mathrm{2}}. \\ $$$${length}\:{of}\:{its}\:{legs}\:{is}\:\sqrt{\mathrm{1}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}. \\ $$$$\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{cos}\:\alpha=\mathrm{1}−\mathrm{2}×\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\alpha=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}\approx\mathrm{70}.\mathrm{529}° \\ $$
Answered by manxsol last updated on 10/Mar/23
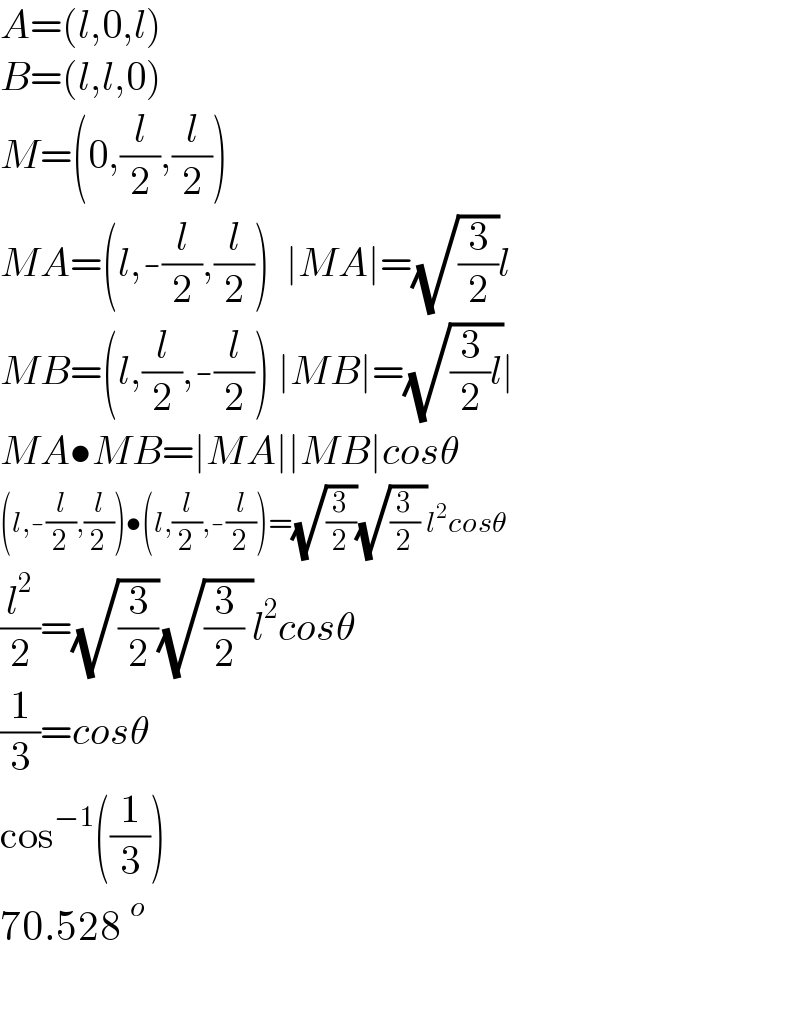
$${A}=\left({l},\mathrm{0},{l}\right) \\ $$$${B}=\left({l},{l},\mathrm{0}\right) \\ $$$${M}=\left(\mathrm{0},\frac{{l}}{\mathrm{2}},\frac{{l}}{\mathrm{2}}\right) \\ $$$${MA}=\left({l},-\frac{{l}}{\mathrm{2}},\frac{{l}}{\mathrm{2}}\right)\:\:\mid{MA}\mid=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}{l} \\ $$$${MB}=\left({l},\frac{{l}}{\mathrm{2}},-\frac{{l}}{\mathrm{2}}\right)\:\mid{MB}\mid=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}{l}}\mid \\ $$$${MA}\bullet{MB}=\mid{MA}\mid\mid{MB}\mid{cos}\theta \\ $$$$\left({l},-\frac{{l}}{\mathrm{2}},\frac{{l}}{\mathrm{2}}\right)\bullet\left({l},\frac{{l}}{\mathrm{2}},-\frac{{l}}{\mathrm{2}}\right)=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}\:}{l}^{\mathrm{2}} {cos}\theta \\ $$$$\frac{{l}^{\mathrm{2}} }{\mathrm{2}}=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}\:}{l}^{\mathrm{2}} {cos}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}={cos}\theta \\ $$$$\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\mathrm{70}.\mathrm{528}\:^{{o}} \\ $$$$ \\ $$
