
Question Number 188861 by Shlock last updated on 08/Mar/23
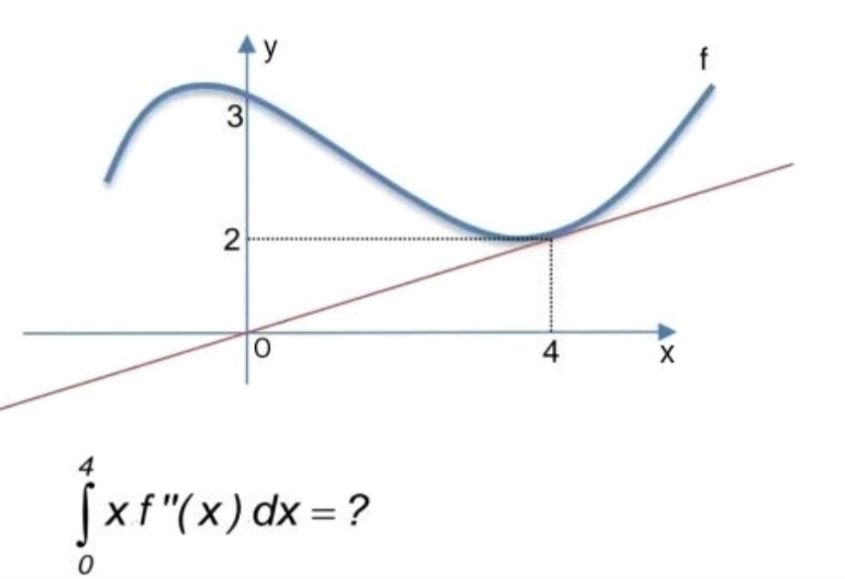
Answered by cortano12 last updated on 08/Mar/23
![∫_0 ^4 x d(f ′(x))= [ x f ′(x)−f(x) ]_0 ^4 = [4 f ′(4)−f(4)+f(0)] = 4.(1/2)−2+3 = 3](Q188873.png)
$$\:\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}\:\mathrm{x}\:\mathrm{d}\left(\mathrm{f}\:'\left(\mathrm{x}\right)\right)=\:\left[\:\mathrm{x}\:\mathrm{f}\:'\left(\mathrm{x}\right)−\mathrm{f}\left(\mathrm{x}\right)\:\right]_{\mathrm{0}} ^{\mathrm{4}} \\ $$$$\:=\:\left[\mathrm{4}\:\mathrm{f}\:'\left(\mathrm{4}\right)−\mathrm{f}\left(\mathrm{4}\right)+\mathrm{f}\left(\mathrm{0}\right)\right] \\ $$$$\:=\:\mathrm{4}.\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}+\mathrm{3}\:=\:\mathrm{3}\: \\ $$
Answered by mr W last updated on 08/Mar/23
![∫^4 _0 xf′′(x)dx =∫^4 _0 xdf′(x) =[xf′(x)]_0 ^4 −∫^4 _0 f′(x)dx =[xf′(x)]_0 ^4 −[f(x)]_0 ^4 =4f′(4)−f(4)+f(0) =4×(2/4)−2+3 =3](Q188874.png)
$$\underset{\mathrm{0}} {\int}^{\mathrm{4}} {xf}''\left({x}\right){dx} \\ $$$$=\underset{\mathrm{0}} {\int}^{\mathrm{4}} {xdf}'\left({x}\right) \\ $$$$=\left[{xf}'\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{4}} −\underset{\mathrm{0}} {\int}^{\mathrm{4}} {f}'\left({x}\right){dx} \\ $$$$=\left[{xf}'\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{4}} −\left[{f}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{4}} \\ $$$$=\mathrm{4}{f}'\left(\mathrm{4}\right)−{f}\left(\mathrm{4}\right)+{f}\left(\mathrm{0}\right) \\ $$$$=\mathrm{4}×\frac{\mathrm{2}}{\mathrm{4}}−\mathrm{2}+\mathrm{3} \\ $$$$=\mathrm{3} \\ $$
