
Question Number 188752 by Soma last updated on 06/Mar/23

Commented by Yacouba last updated on 06/Mar/23
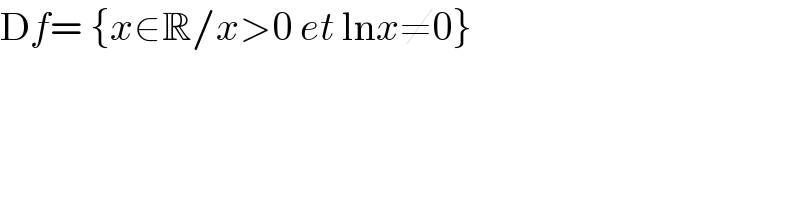
$$\mathrm{D}{f}=\:\left\{{x}\in\mathbb{R}/{x}>\mathrm{0}\:{et}\:\mathrm{ln}{x}\neq\mathrm{0}\right\} \\ $$
Answered by a.lgnaoui last updated on 06/Mar/23
![1•D_f ={x/x∈R^(∗+) et x≠1} D_f =]0,1[∪]1,+∞[ 2•limf(x)_(x→0^+ ) =lim_(x→0^+ ) (1−(1/(lnx))) =1−lim_(x→0^+ ) ((1/(lnx)) )=1 • limf(x)_(x→1^− ) =lim_(x→1^− ) ((−1)/(lnx))=+∞ •limf(x)_(x→1^+ ) =−∞ •limf(x)_(x→+∞) =lim_(x→+∞) ((x[(lnx+((lnx)/x))−(1/x)])/(lnx))= =lim((xlnx)/(lnx))=+∞ =lim((xlnx)/(lnx)) 3•lim(f(x)−x)_(x→+∞) =1−((1/(lnx)))=1 donc au voisinage de +∞:f(x)≅x+1 x+1 est donc Asymptote a la courbe de f(x). •x=0 x=1 (aussi asymptotes) 4•(f(x)−(x+1)=((−1)/(lnx))<0 donc l asymptote[est au dessous de courbe(C) 5•f^′ (x)=1−((1/(lnx)))^′ =1+(1/(x(lnx)^2 )) 6•x>0⇒f^′ (x)>0 :(f(x) croissante) 7•tengenteℸa (C) au point x=e est f(x)−f(e)=(x−e)f_(x=e) ^: (x) f(e)=e ⇒f′(e)=((e^2 +1)/e) (x+1−(1/(lnx)))−e=((e^2 +1)/e)(x−e) l equation est : x(1−((e^2 +1)/e))−(1/(lnx))+e^2 +1=0 8•Voir la courbe (C)](Q188768.png)
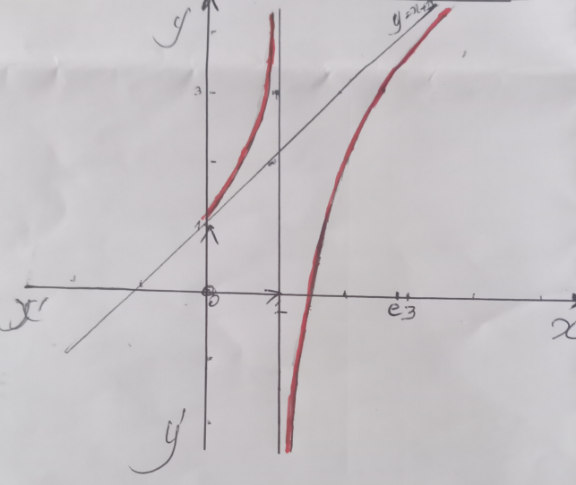
$$\mathrm{1}\bullet{D}_{{f}} =\left\{{x}/{x}\in\mathbb{R}^{\ast+} \:{et}\:{x}\neq\mathrm{1}\right\} \\ $$$$\left.\:\:\:\:\:\:\:{D}_{{f}} \:\:=\right]\mathrm{0},\mathrm{1}\left[\cup\right]\mathrm{1},+\infty\left[\right. \\ $$$$\mathrm{2}\bullet{limf}\left({x}\right)_{{x}\rightarrow\mathrm{0}^{+} } ={lim}_{{x}\rightarrow\mathrm{0}^{+} } \left(\mathrm{1}−\frac{\mathrm{1}}{{lnx}}\right) \\ $$$$=\mathrm{1}−{lim}_{{x}\rightarrow\mathrm{0}^{+} } \left(\frac{\mathrm{1}}{{lnx}}\:\:\right)=\mathrm{1} \\ $$$$\:\:\:\bullet\:{limf}\left({x}\right)_{{x}\rightarrow\mathrm{1}^{−} } ={lim}_{{x}\rightarrow\mathrm{1}^{−} } \frac{−\mathrm{1}}{{lnx}}=+\infty \\ $$$$\:\:\:\bullet{limf}\left({x}\right)_{{x}\rightarrow\mathrm{1}^{+} } =−\infty \\ $$$$\:\:\:\bullet{limf}\left({x}\right)_{{x}\rightarrow+\infty} ={lim}_{{x}\rightarrow+\infty} \frac{{x}\left[\left({lnx}+\frac{{lnx}}{{x}}\right)−\frac{\mathrm{1}}{{x}}\right]}{{lnx}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={lim}\frac{{xlnx}}{{lnx}}=+\infty \\ $$$$\:\:\:\:\:\:\:\:={lim}\frac{{xlnx}}{{lnx}} \\ $$$$\mathrm{3}\bullet{lim}\left({f}\left({x}\right)−{x}\right)_{{x}\rightarrow+\infty} =\mathrm{1}−\left(\frac{\mathrm{1}}{{lnx}}\right)=\mathrm{1} \\ $$$${donc}\:\:{au}\:{voisinage}\:{de}\:+\infty:{f}\left({x}\right)\cong{x}+\mathrm{1} \\ $$$$\boldsymbol{{x}}+\mathrm{1}\:{est}\:{donc}\:{Asymptote}\:{a}\:{la}\:{courbe}\:{de}\:{f}\left({x}\right). \\ $$$$\:\bullet\boldsymbol{{x}}=\mathrm{0}\:\:\:\:\boldsymbol{{x}}=\mathrm{1}\:\left({aussi}\:{asymptotes}\right) \\ $$$$\mathrm{4}\bullet\left({f}\left({x}\right)−\left({x}+\mathrm{1}\right)=\frac{−\mathrm{1}}{{lnx}}<\mathrm{0}\right. \\ $$$${donc}\:\:\:{l}\:{asymptote}\left[{est}\:\boldsymbol{{au}}\:\boldsymbol{{dessous}}\:\boldsymbol{{de}}\:\boldsymbol{{courbe}}\left(\boldsymbol{{C}}\right)\right. \\ $$$$\mathrm{5}\bullet{f}^{'} \left({x}\right)=\mathrm{1}−\left(\frac{\mathrm{1}}{{lnx}}\right)^{'} =\mathrm{1}+\frac{\mathrm{1}}{{x}\left({lnx}\right)^{\mathrm{2}} } \\ $$$$\mathrm{6}\bullet{x}>\mathrm{0}\Rightarrow{f}^{'} \left({x}\right)>\mathrm{0}\::\left({f}\left({x}\right)\:{croissante}\right) \\ $$$$\mathrm{7}\bullet{tengente}\daleth{a}\:\left({C}\right)\:{au}\:{point}\:\boldsymbol{{x}}=\boldsymbol{{e}}\:{est} \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)−\boldsymbol{{f}}\left(\boldsymbol{{e}}\right)=\left(\boldsymbol{{x}}−\boldsymbol{{e}}\right)\boldsymbol{{f}}_{{x}={e}} ^{:} \left({x}\right) \\ $$$$ \\ $$$${f}\left({e}\right)={e}\:\:\:\Rightarrow{f}'\left({e}\right)=\frac{{e}^{\mathrm{2}} +\mathrm{1}}{{e}} \\ $$$$\:\:\:\:\left({x}+\mathrm{1}−\frac{\mathrm{1}}{{lnx}}\right)−{e}=\frac{{e}^{\mathrm{2}} +\mathrm{1}}{{e}}\left({x}−{e}\right) \\ $$$${l}\:{equation}\:{est}\:: \\ $$$$\boldsymbol{{x}}\left(\mathrm{1}−\frac{\boldsymbol{{e}}^{\mathrm{2}} +\mathrm{1}}{\boldsymbol{{e}}}\right)−\frac{\mathrm{1}}{\boldsymbol{{lnx}}}+\boldsymbol{{e}}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{8}\bullet{Voir}\:\:\:{la}\:{courbe}\:\:\left({C}\right) \\ $$
Commented by a.lgnaoui last updated on 06/Mar/23
Commented by a.lgnaoui last updated on 06/Mar/23
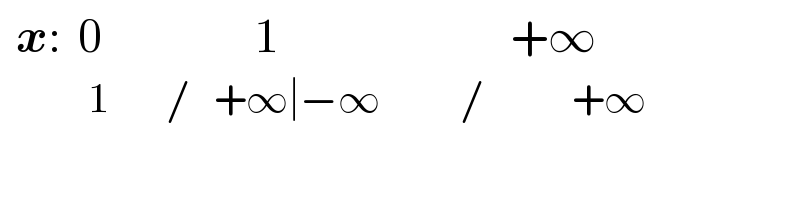
$$\:\:\boldsymbol{{x}}:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:/\:\:\:+\infty\mid−\infty\:\:\:\:\:\:\:\:\:\:/\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$
