
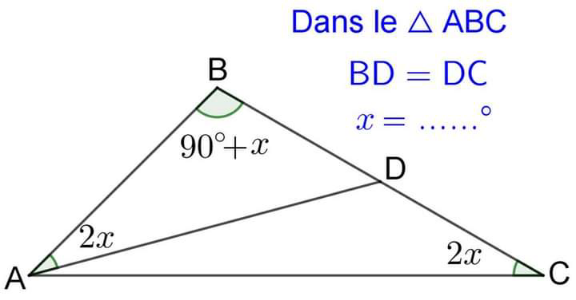
Question Number 188701 by cortano12 last updated on 05/Mar/23
Commented by mr W last updated on 06/Mar/23

$${x}=\mathrm{15}° \\ $$
Commented by cortano12 last updated on 07/Mar/23

$$\mathrm{yes} \\ $$
Answered by a.lgnaoui last updated on 05/Mar/23
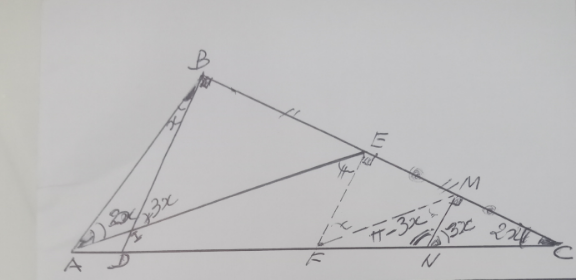
![△ABE △BIE ∡BIE=3x BD ∥EF∥MN⇒(∡DBE=∡FEM=∡NMC=90)[∡B=90+x] △NMC triangle rectangle en M ⇒∡FNM−∡CNN=∡NCM+90 180−3x=2x+90 x=18°](Q188713.png)
$$\bigtriangleup{ABE}\:\:\:\bigtriangleup{BIE}\:\:\:\measuredangle{BIE}=\mathrm{3}{x} \\ $$$${BD}\:\parallel{EF}\parallel{MN}\Rightarrow\left(\measuredangle{DBE}=\measuredangle{FEM}=\measuredangle{NMC}=\mathrm{90}\right)\left[\measuredangle{B}=\mathrm{90}+{x}\right] \\ $$$$\bigtriangleup{NMC}\:{triangle}\:{rectangle}\:{en}\:{M} \\ $$$$\Rightarrow\measuredangle{FNM}−\measuredangle{CNN}=\measuredangle{NCM}+\mathrm{90} \\ $$$$\:\:\:\:\mathrm{180}−\mathrm{3}{x}=\mathrm{2}{x}+\mathrm{90}\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{x}}=\mathrm{18}° \\ $$
Commented by a.lgnaoui last updated on 05/Mar/23
Commented by mr W last updated on 06/Mar/23
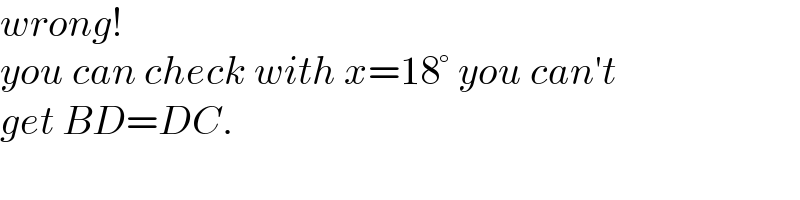
$${wrong}! \\ $$$${you}\:{can}\:{check}\:{with}\:{x}=\mathrm{18}°\:{you}\:{can}'{t} \\ $$$${get}\:{BD}={DC}. \\ $$
Commented by mehdee42 last updated on 06/Mar/23

$${this}\:{value}\:{cannot}\:{be}\:{correct}\:{according}\:{to}\:{the}\:{shape} \\ $$
Answered by mehdee42 last updated on 06/Mar/23
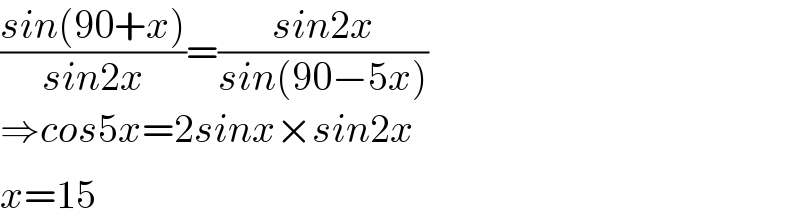
$$\frac{{sin}\left(\mathrm{90}+{x}\right)}{{sin}\mathrm{2}{x}}=\frac{{sin}\mathrm{2}{x}}{{sin}\left(\mathrm{90}−\mathrm{5}{x}\right)} \\ $$$$\Rightarrow{cos}\mathrm{5}{x}=\mathrm{2}{sinx}×{sin}\mathrm{2}{x} \\ $$$${x}=\mathrm{15}^{} \\ $$
