
Question Number 18866 by mondodotto@gmail.com last updated on 31/Jul/17
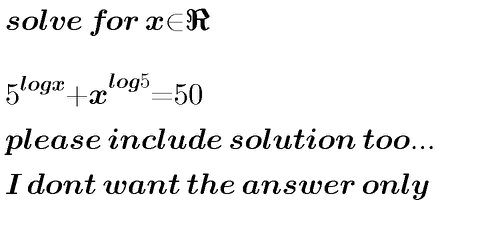
Answered by dioph last updated on 31/Jul/17
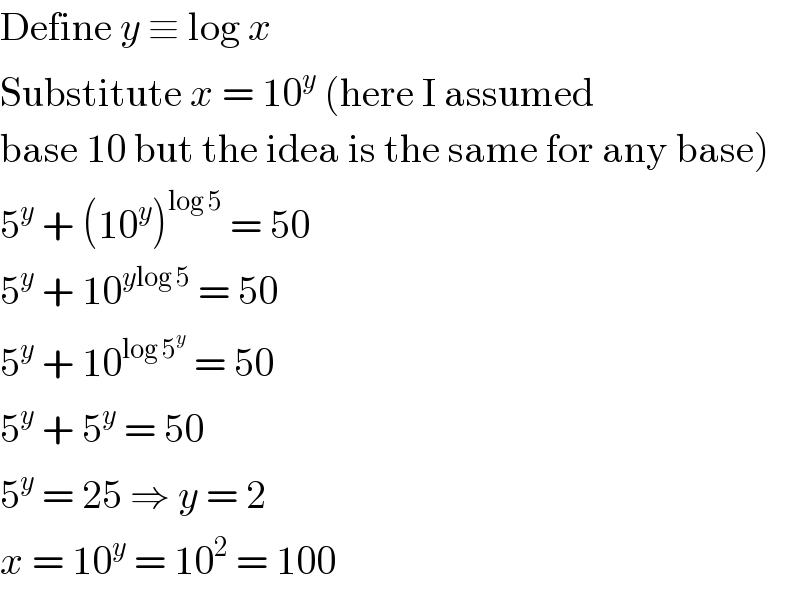
$$\mathrm{Define}\:{y}\:\equiv\:\mathrm{log}\:{x} \\ $$$$\mathrm{Substitute}\:{x}\:=\:\mathrm{10}^{{y}} \:\left(\mathrm{here}\:\mathrm{I}\:\mathrm{assumed}\right. \\ $$$$\left.\mathrm{base}\:\mathrm{10}\:\mathrm{but}\:\mathrm{the}\:\mathrm{idea}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{for}\:\mathrm{any}\:\mathrm{base}\right) \\ $$$$\mathrm{5}^{{y}} \:+\:\left(\mathrm{10}^{{y}} \right)^{\mathrm{log}\:\mathrm{5}} \:=\:\mathrm{50} \\ $$$$\mathrm{5}^{{y}} \:+\:\mathrm{10}^{{y}\mathrm{log}\:\mathrm{5}} \:=\:\mathrm{50} \\ $$$$\mathrm{5}^{{y}} \:+\:\mathrm{10}^{\mathrm{log}\:\mathrm{5}^{{y}} } \:=\:\mathrm{50} \\ $$$$\mathrm{5}^{{y}} \:+\:\mathrm{5}^{{y}} \:=\:\mathrm{50} \\ $$$$\mathrm{5}^{{y}} \:=\:\mathrm{25}\:\Rightarrow\:{y}\:=\:\mathrm{2} \\ $$$${x}\:=\:\mathrm{10}^{{y}} \:=\:\mathrm{10}^{\mathrm{2}} \:=\:\mathrm{100} \\ $$
