Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 188646 by Rupesh123 last updated on 04/Mar/23

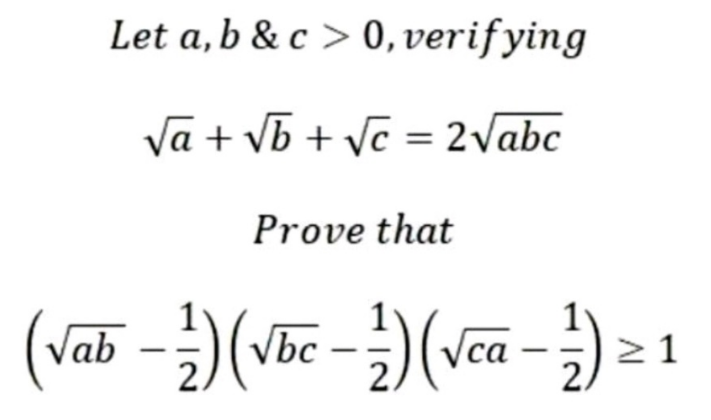
Answered by Frix last updated on 04/Mar/23

Due to symmetry the minimum of ((√(ab))−(1/2))((√(ac))−(1/2))((√(bc))−(1/2)) is at c=b=a ⇒ 3(√a)=2a(√a) ⇒ a=(3/2) The minimum is 1 [btw. (√u)=(((√v)+(√w))/(2(√(vw))−1)) ⇒ (√(ab)), (√(ac)), (√(bc))>(1/2)]

$$\mathrm{Due}\:\mathrm{to}\:\mathrm{symmetry}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{of} \\ $$$$\left(\sqrt{{ab}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\sqrt{{ac}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\sqrt{{bc}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\:\mathrm{is}\:\mathrm{at} \\ $$$${c}={b}={a} \\ $$$$\Rightarrow \\ $$$$\mathrm{3}\sqrt{{a}}=\mathrm{2}{a}\sqrt{{a}}\:\Rightarrow\:{a}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{minimum}\:\mathrm{is}\:\mathrm{1} \\ $$$$\left[\mathrm{btw}.\:\sqrt{{u}}=\frac{\sqrt{{v}}+\sqrt{{w}}}{\mathrm{2}\sqrt{{vw}}−\mathrm{1}}\:\Rightarrow\:\sqrt{{ab}},\:\sqrt{{ac}},\:\sqrt{{bc}}>\frac{\mathrm{1}}{\mathrm{2}}\right] \\ $$

Commented by Rupesh123 last updated on 04/Mar/23

Nice, sir!

Answered by mehdee42 last updated on 04/Mar/23

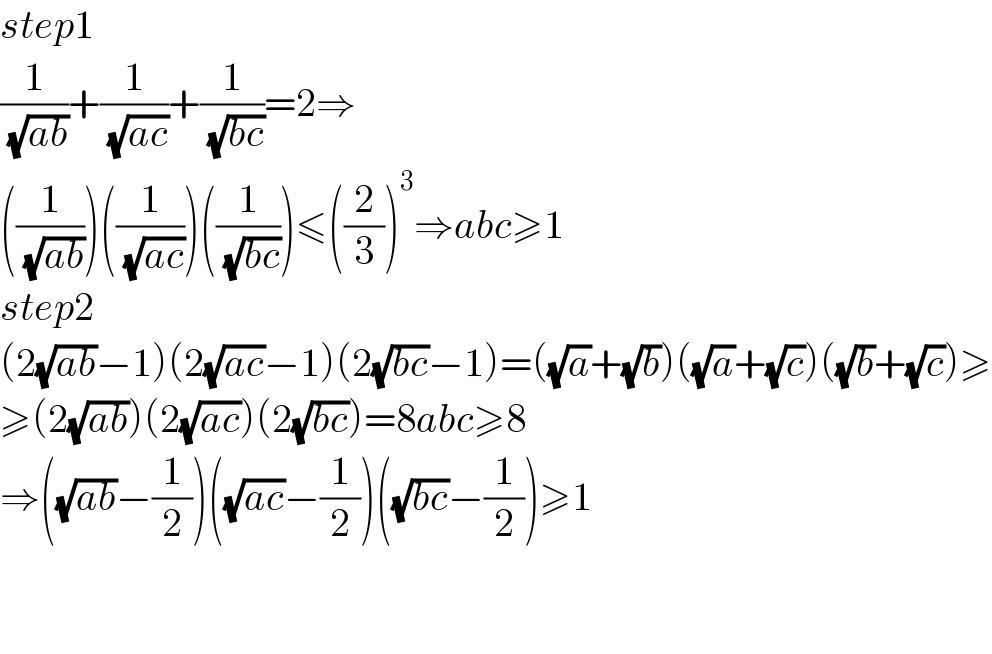
step1 (1/( (√(ab))))+(1/( (√(ac))))+(1/( (√(bc))))=2⇒ ((1/( (√(ab)))))((1/( (√(ac)))))((1/( (√(bc)))))≤((2/3))^3 ⇒abc≥1 step2 (2(√(ab))−1)(2(√(ac))−1)(2(√(bc))−1)=((√a)+(√b))((√a)+(√c))((√b)+(√c))≥ ≥(2(√(ab)))(2(√(ac)))(2(√(bc)))=8abc≥8 ⇒((√(ab))−(1/2))((√(ac))−(1/2))((√(bc))−(1/2))≥1

$${step}\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{ab}}}+\frac{\mathrm{1}}{\:\sqrt{{ac}}}+\frac{\mathrm{1}}{\:\sqrt{{bc}}}=\mathrm{2}\Rightarrow \\ $$$$\left(\frac{\mathrm{1}}{\:\sqrt{{ab}}}\right)\left(\frac{\mathrm{1}}{\:\sqrt{{ac}}}\right)\left(\frac{\mathrm{1}}{\:\sqrt{{bc}}}\right)\leqslant\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{3}} \Rightarrow{abc}\geqslant\mathrm{1} \\ $$$${step}\mathrm{2} \\ $$$$\left(\mathrm{2}\sqrt{{ab}}−\mathrm{1}\right)\left(\mathrm{2}\sqrt{{ac}}−\mathrm{1}\right)\left(\mathrm{2}\sqrt{{bc}}−\mathrm{1}\right)=\left(\sqrt{{a}}+\sqrt{{b}}\right)\left(\sqrt{{a}}+\sqrt{{c}}\right)\left(\sqrt{{b}}+\sqrt{{c}}\right)\geqslant \\ $$$$\geqslant\left(\mathrm{2}\sqrt{{ab}}\right)\left(\mathrm{2}\sqrt{{ac}}\right)\left(\mathrm{2}\sqrt{{bc}}\right)=\mathrm{8}{abc}\geqslant\mathrm{8} \\ $$$$\Rightarrow\left(\sqrt{{ab}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\sqrt{{ac}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\sqrt{{bc}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\geqslant\mathrm{1} \\ $$$$ \\ $$$$ \\ $$

Commented by Rupesh123 last updated on 04/Mar/23

Nice, sir!

Terms of Service

Privacy Policy

Contact: info@tinkutara.com